 por Thyago Quimica » Dom Out 21, 2012 14:53
por Thyago Quimica » Dom Out 21, 2012 14:53
Esboce o grafico de

o Que eu fiz:
1) D = R - {0}
2)
![f'(x)= 2x-\frac{1}{{x}^{2}}\Rightarrow\frac{2{x}^{3}-1}{{x}^{2}}\Rightarrow 2{x}^{3}-1=0\Rightarrow x=\sqrt[3]{\frac{1}{2}} f'(x)= 2x-\frac{1}{{x}^{2}}\Rightarrow\frac{2{x}^{3}-1}{{x}^{2}}\Rightarrow 2{x}^{3}-1=0\Rightarrow x=\sqrt[3]{\frac{1}{2}}](/latexrender/pictures/bb5ab419de979e35beedb26dfa6f2a5a.png)
substitui o valor encontrado na f '(x) em f(x) para encontrar o Ponto Critico
![f(\sqrt[3]{\frac{1}{2}})= {\left(\sqrt[3]{\frac{1}{2}} \right)}^{2}+ \frac{1}{\sqrt[3]{\frac{1}{2}}} f(\sqrt[3]{\frac{1}{2}})= {\left(\sqrt[3]{\frac{1}{2}} \right)}^{2}+ \frac{1}{\sqrt[3]{\frac{1}{2}}}](/latexrender/pictures/9e0e5d4473abe6e5830356c596b47c66.png)
Mais nao consegui resolver mais, para dai estudar as regios de crescimento e decrescimento.
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por MrJuniorFerr » Dom Out 21, 2012 20:36
por MrJuniorFerr » Dom Out 21, 2012 20:36
"substitui o valor encontrado na
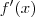
em

para encontrar o Ponto Critico"
Você deve estar confundindo as coisas meu amigo...
pontos críticos são valores de x que zeram
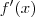
ou valores de x que a

não existe.
Se você substituir o ponto crítico encontrado na função

, você vai encontrar um possível máx ou mín global.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 21, 2012 21:46
por MarceloFantini » Dom Out 21, 2012 21:46
Ao substituir o valor de

encontrado ao resolver
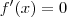
, você apenas encontrará o valor da função correspondente a um máximo ou mínimo
local.
Para esboçar o gráfico, você precisa encontrar agora os valores onde

e
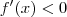
. Eles serão, respectivamente, os valores onde a função é crescente e decrescente.
Após isso, encontre

para determinar os pontos de inflexão. Os pontos onde

e

serão os intervalos onde a função é convexa e côncava, respectivamente.
Finalmente, depois de tudo isto, você poderá esboçar o gráfico.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Gustavo Gomes » Dom Out 21, 2012 21:52
por Gustavo Gomes » Dom Out 21, 2012 21:52
Olá, Thyago.
Note que
![f\left( \sqrt[3]{\frac{1}{2}} \right)=\left( {\sqrt[3]{\frac{1}{2}}} \right)^{2}+\frac{1}{\sqrt[3]{\frac{1}{2}}}=\frac{1}{\sqrt[3]{4}}+\sqrt[3]{2}=\frac{1+\sqrt[3]{8}}{\sqrt[3]{4}}=\frac{3}{\sqrt[3]{4}}=\frac{3\sqrt[3]{2}}{2} f\left( \sqrt[3]{\frac{1}{2}} \right)=\left( {\sqrt[3]{\frac{1}{2}}} \right)^{2}+\frac{1}{\sqrt[3]{\frac{1}{2}}}=\frac{1}{\sqrt[3]{4}}+\sqrt[3]{2}=\frac{1+\sqrt[3]{8}}{\sqrt[3]{4}}=\frac{3}{\sqrt[3]{4}}=\frac{3\sqrt[3]{2}}{2}](/latexrender/pictures/e027f53073fce213c5ed64a9e3d3bcfd.png)
, que é um possível valor máximo/mínimo local de f.
Basta dar continuidade à análise.
Abraço.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Estudo do Gráfico
por Fernandobertolaccini » Qua Out 29, 2014 15:31
- 0 Respostas
- 626 Exibições
- Última mensagem por Fernandobertolaccini

Qua Out 29, 2014 15:31
Cálculo: Limites, Derivadas e Integrais
-
- [gráfico] Estudo das Funções
por Cleyson007 » Sáb Set 06, 2008 01:45
- 3 Respostas
- 4159 Exibições
- Última mensagem por admin

Ter Set 09, 2008 15:46
Funções
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:17
- 2 Respostas
- 2096 Exibições
- Última mensagem por adauto martins

Qui Dez 18, 2014 11:43
Geometria Analítica
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:21
- 0 Respostas
- 1358 Exibições
- Última mensagem por Livingstone

Sex Dez 12, 2014 15:21
Geometria Analítica
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:27
- 1 Respostas
- 1568 Exibições
- Última mensagem por adauto martins

Ter Dez 16, 2014 10:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![f'(x)= 2x-\frac{1}{{x}^{2}}\Rightarrow\frac{2{x}^{3}-1}{{x}^{2}}\Rightarrow 2{x}^{3}-1=0\Rightarrow x=\sqrt[3]{\frac{1}{2}} f'(x)= 2x-\frac{1}{{x}^{2}}\Rightarrow\frac{2{x}^{3}-1}{{x}^{2}}\Rightarrow 2{x}^{3}-1=0\Rightarrow x=\sqrt[3]{\frac{1}{2}}](/latexrender/pictures/bb5ab419de979e35beedb26dfa6f2a5a.png)
![f(\sqrt[3]{\frac{1}{2}})= {\left(\sqrt[3]{\frac{1}{2}} \right)}^{2}+ \frac{1}{\sqrt[3]{\frac{1}{2}}} f(\sqrt[3]{\frac{1}{2}})= {\left(\sqrt[3]{\frac{1}{2}} \right)}^{2}+ \frac{1}{\sqrt[3]{\frac{1}{2}}}](/latexrender/pictures/9e0e5d4473abe6e5830356c596b47c66.png)


![f'(x)= 2x-\frac{1}{{x}^{2}}\Rightarrow\frac{2{x}^{3}-1}{{x}^{2}}\Rightarrow 2{x}^{3}-1=0\Rightarrow x=\sqrt[3]{\frac{1}{2}} f'(x)= 2x-\frac{1}{{x}^{2}}\Rightarrow\frac{2{x}^{3}-1}{{x}^{2}}\Rightarrow 2{x}^{3}-1=0\Rightarrow x=\sqrt[3]{\frac{1}{2}}](/latexrender/pictures/bb5ab419de979e35beedb26dfa6f2a5a.png)
![f(\sqrt[3]{\frac{1}{2}})= {\left(\sqrt[3]{\frac{1}{2}} \right)}^{2}+ \frac{1}{\sqrt[3]{\frac{1}{2}}} f(\sqrt[3]{\frac{1}{2}})= {\left(\sqrt[3]{\frac{1}{2}} \right)}^{2}+ \frac{1}{\sqrt[3]{\frac{1}{2}}}](/latexrender/pictures/9e0e5d4473abe6e5830356c596b47c66.png)

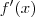 em
em  para encontrar o Ponto Critico"
para encontrar o Ponto Critico"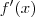 ou valores de x que a
ou valores de x que a  não existe.
não existe. , você vai encontrar um possível máx ou mín global.
, você vai encontrar um possível máx ou mín global.
 encontrado ao resolver
encontrado ao resolver 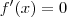 , você apenas encontrará o valor da função correspondente a um máximo ou mínimo local.
, você apenas encontrará o valor da função correspondente a um máximo ou mínimo local. e
e 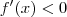 . Eles serão, respectivamente, os valores onde a função é crescente e decrescente.
. Eles serão, respectivamente, os valores onde a função é crescente e decrescente. para determinar os pontos de inflexão. Os pontos onde
para determinar os pontos de inflexão. Os pontos onde  e
e  serão os intervalos onde a função é convexa e côncava, respectivamente.
serão os intervalos onde a função é convexa e côncava, respectivamente.

![f\left( \sqrt[3]{\frac{1}{2}} \right)=\left( {\sqrt[3]{\frac{1}{2}}} \right)^{2}+\frac{1}{\sqrt[3]{\frac{1}{2}}}=\frac{1}{\sqrt[3]{4}}+\sqrt[3]{2}=\frac{1+\sqrt[3]{8}}{\sqrt[3]{4}}=\frac{3}{\sqrt[3]{4}}=\frac{3\sqrt[3]{2}}{2} f\left( \sqrt[3]{\frac{1}{2}} \right)=\left( {\sqrt[3]{\frac{1}{2}}} \right)^{2}+\frac{1}{\sqrt[3]{\frac{1}{2}}}=\frac{1}{\sqrt[3]{4}}+\sqrt[3]{2}=\frac{1+\sqrt[3]{8}}{\sqrt[3]{4}}=\frac{3}{\sqrt[3]{4}}=\frac{3\sqrt[3]{2}}{2}](/latexrender/pictures/e027f53073fce213c5ed64a9e3d3bcfd.png) , que é um possível valor máximo/mínimo local de f.
, que é um possível valor máximo/mínimo local de f. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.