obs: Me parece que o editor de fórmulas está com problemas, ou eu não soube utiliza-lo corretamente.
![\lim_{+\propto}(x-\sqrt[]{x+3}) \lim_{+\propto}(x-\sqrt[]{x+3})](/latexrender/pictures/42c0f95f3ff234361c5155230ba855a9.png)
![=\frac{(x-\sqrt[]{x+3})(x+\sqrt[]{x+3})}{x+\sqrt[]{x+3}} =\frac{(x-\sqrt[]{x+3})(x+\sqrt[]{x+3})}{x+\sqrt[]{x+3}}](/latexrender/pictures/146892f0a230ad7ab2befcd003ae5da6.png) Devido a indeterminação que ocorre acima, multipliquei pelo conjugado.
Devido a indeterminação que ocorre acima, multipliquei pelo conjugado.![=\frac{{x}^{2}(1-\frac{1}{x}-\frac{3}{x}}{x+\sqrt[]{x(1+\frac{3}{x})}} =\frac{{x}^{2}(1-\frac{1}{x}-\frac{3}{x}}{x+\sqrt[]{x(1+\frac{3}{x})}}](/latexrender/pictures/b007e6edeab150ce0ae67710f03d14b7.png) Daí então cheguei a um resultado e já simplifiquei dessa maneira.
Daí então cheguei a um resultado e já simplifiquei dessa maneira.![=\frac{\sqrt[1]{{x}^{2}}}{\sqrt[]{x}+x} =\frac{\sqrt[1]{{x}^{2}}}{\sqrt[]{x}+x}](/latexrender/pictures/ac6b5901064ac041da01c40941ed7b92.png) Daí eu resolvi fazer essa divisão de radicais porque em cima não consegui evitar a indeterminação. (Essa é minha dúvida não sei se posso fazer isso).
Daí eu resolvi fazer essa divisão de radicais porque em cima não consegui evitar a indeterminação. (Essa é minha dúvida não sei se posso fazer isso).![=\sqrt[3]{x}+x = +\propto =\sqrt[3]{x}+x = +\propto](/latexrender/pictures/30b95c169c7593e762e1526820f94393.png) Chegando ao resultado da divisão de radicais e finalmente ao resultado final(+infinito).
Chegando ao resultado da divisão de radicais e finalmente ao resultado final(+infinito).Então essa é minha dúvida amigos, não sei se existe algo na teoria do assunto de limites que me impeça de fazer aquela divisão de radicais(na segunda sentença de baixo para cima), mas eu fiz a divisão utilizando as propriedades e evitei a indeterminação.
Muito obrigado, e para o pessoal do nordeste fiquem atentos que em novembro tem três congressos, um em Salvador, um em Natal e outro em João Pessoa, entre no site da SBM e confira.
Um abraço a todos.


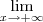 em todos os passos. Você deve escrever essa notação em todos os passos, exceto no último, quando você efetivamente calcula o valor do limite. Desse modo, você deveria ter escrito:
em todos os passos. Você deve escrever essa notação em todos os passos, exceto no último, quando você efetivamente calcula o valor do limite. Desse modo, você deveria ter escrito: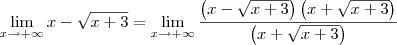



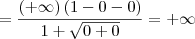

![x(1+\sqrt[]{\frac{1}{x}+\frac{3}{{x}^{2}}}) x(1+\sqrt[]{\frac{1}{x}+\frac{3}{{x}^{2}}})](/latexrender/pictures/c45e2860670db63d90bc9c8033ff3be7.png)
![\frac{{x}^{2}}{\sqrt[]{x}}=\frac{\sqrt[1]{{x}^{2}}}{\sqrt[]{x}}=\frac{\sqrt[]{{x}^{4}}}{\sqrt[]{x}}=\sqrt[]{\frac{{x}^{4}}{x}}=\sqrt[]{{x}^{3}} \frac{{x}^{2}}{\sqrt[]{x}}=\frac{\sqrt[1]{{x}^{2}}}{\sqrt[]{x}}=\frac{\sqrt[]{{x}^{4}}}{\sqrt[]{x}}=\sqrt[]{\frac{{x}^{4}}{x}}=\sqrt[]{{x}^{3}}](/latexrender/pictures/1dccd14fcfc3f1ba2f08c86831c13924.png) Tem algum erro nesta sentença?
Tem algum erro nesta sentença?![x + \sqrt{x\left(1 + \frac{3}{x}\right)} = x\left[1 + \frac{1}{x}\sqrt{x\left(1 + \frac{3}{x}\right)}\right] x + \sqrt{x\left(1 + \frac{3}{x}\right)} = x\left[1 + \frac{1}{x}\sqrt{x\left(1 + \frac{3}{x}\right)}\right]](/latexrender/pictures/5f1ea2b03d195d75a1f079083626308e.png)
![= x\left[1 + \sqrt{\frac{x}{x^2}\left(1 + \frac{3}{x}\right)}\right] = x\left[1 + \sqrt{\frac{x}{x^2}\left(1 + \frac{3}{x}\right)}\right]](/latexrender/pictures/71de11a81ef3e031cae2c926aff1bced.png)
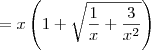
![\frac{\sqrt[1]{x^2}}{\sqrt{x}+x} \frac{\sqrt[1]{x^2}}{\sqrt{x}+x}](/latexrender/pictures/8c2bdecf485b141bfcdb2d3c8b44802a.png) seria o mesmo que
seria o mesmo que ![\frac{\sqrt[1]{x^2}}{\sqrt{x}} + \frac{\sqrt[1]{x^2}}{x} \frac{\sqrt[1]{x^2}}{\sqrt{x}} + \frac{\sqrt[1]{x^2}}{x}](/latexrender/pictures/d955e2ec4363257646841bbe442f1f51.png) , mas isso está errado. E mesmo ao cometer esse erro, você ainda cometeu outro: escreveu
, mas isso está errado. E mesmo ao cometer esse erro, você ainda cometeu outro: escreveu ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) ao invés de
ao invés de  .
.![=\frac{{x}^{2}(1-\frac{1}{x}-\frac{3}{x})}{x+\sqrt[]{x(1+\frac{3}{x})}} =\frac{{x}^{2}(1-\frac{1}{x}-\frac{3}{x})}{x+\sqrt[]{x(1+\frac{3}{x})}}](/latexrender/pictures/4492dee1332de9f12896a00df0c56ddc.png)
![=\frac{\sqrt[1]{{x}^{2}}}{\sqrt[]{x}+x}=\sqrt[]{{x}^{3}}+x = +\propto =\frac{\sqrt[1]{{x}^{2}}}{\sqrt[]{x}+x}=\sqrt[]{{x}^{3}}+x = +\propto](/latexrender/pictures/7b3141d87631ce791064e82c58b11149.png)
![=\frac{x(1-\frac{1}{x}-\frac{3}{x})}{\sqrt[]{x(1+\frac{3}{x})}} =\frac{x(1-\frac{1}{x}-\frac{3}{x})}{\sqrt[]{x(1+\frac{3}{x})}}](/latexrender/pictures/cdee5b545900328877557cc0f46d1f68.png)
![=\frac{x}{\sqrt[]{x}} =\frac{x}{\sqrt[]{x}}](/latexrender/pictures/4658830d44e623e2a8e2bdbbc8ade0e2.png)
![=\sqrt[]{x}=+\propto =\sqrt[]{x}=+\propto](/latexrender/pictures/3782b8fdc952a391de76435df3759ca7.png)
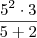
 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
