
E eu estava reescrevendo na forma:
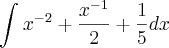
Mas não tenho certeza se isso esta certo, se eu posso escreve-la assim, pois:
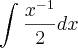
Vai dar uma indeterminação do tipo 1/0, então pesso ajuda nisso ai...É o caminho certo, ou devo usar outros métodos, se devo usar então de que jeito??
obrigado!!



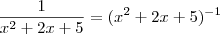
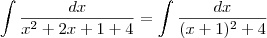
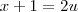
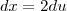
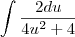


 . Tome
. Tome  para ver, a primeira expressão resulta em
para ver, a primeira expressão resulta em  enquanto que a outra nem está definida.
enquanto que a outra nem está definida. e faça a substituição
e faça a substituição 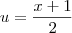 .
.
