indeterminação do tipo
- A resposta é 1/2, a minha está dando 0
Eu igualei os denominadores e apliquei L'hopital , derivando o numerador e o denominador (logicamente sem usar a regra da derivada para quociente).
Alguém me ajuda a visualizar onde errei?
att. Sammy
Ps.: limite em anexo
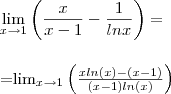.![\lim_{x\to 1}\left(\frac{x ln(x) - (x-1)}{(x-1)ln(x)} \right) = \lim_{x\to1} \left[\frac{\mathrm{d^2} }{\mathrm{d} x^2}\left( \frac{x ln(x) - (x-1)}{(x- 1)ln(x)}\right ) \right ]](/latexrender/pictures/0caee27a19890c2a06dcae6fdb4fe3dc.png "\lim_{x\to 1}\left(\frac{x ln(x) - (x-1)}{(x-1)ln(x)} \right) = \lim_{x\to1} \left[\frac{\mathrm{d^2} }{\mathrm{d} x^2}\left( \frac{x ln(x) - (x-1)}{(x- 1)ln(x)}\right ) \right ]")
.Assim , obtemos :
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)