 por Russman » Sex Jul 20, 2012 12:36
por Russman » Sex Jul 20, 2012 12:36
Eu procurei sem sucesso uma fórmula fechada para a derivada n-ésima total de um produto de N funções! Isto é, eu gostaria de encontrar uma fórmula fechada para a n-ésima derivada de :
![\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\left [f_{1}(x).f_{2}(x).\cdot \cdot \cdot f_{N}(x) \right ]=\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\prod_{j=1}^{N}f_{i}(x) = ? \frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\left [f_{1}(x).f_{2}(x).\cdot \cdot \cdot f_{N}(x) \right ]=\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\prod_{j=1}^{N}f_{i}(x) = ?](/latexrender/pictures/7d406c2be6b194be99b00e6387bac8e7.png)
Obrigado pela parceria.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Sex Jul 20, 2012 16:47
por e8group » Sex Jul 20, 2012 16:47
Russman . Não sei se vai te ajudar ,mas não seria isto ?
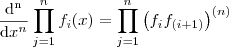
,onde :
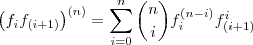
Uso da notação (n) significa derivar n-vezes .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sex Jul 20, 2012 22:49
por Russman » Sex Jul 20, 2012 22:49
Obrigado, Shantiago. Mas eu acredito que a fórmula não esteja certa. ;x
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ajuste Exponencial] Fórmula fechada
por avulsonasociedade » Sex Jun 08, 2012 11:26
- 1 Respostas
- 1355 Exibições
- Última mensagem por MarceloFantini

Qua Jun 13, 2012 20:22
Geometria Analítica
-
- fórmula
por Ismafa » Ter Fev 17, 2009 01:29
- 2 Respostas
- 3227 Exibições
- Última mensagem por Ismafa

Qua Fev 25, 2009 09:57
Sistemas de Equações
-
- Fórmula de PMT
por Leonardonc » Seg Ago 27, 2012 09:27
- 0 Respostas
- 2277 Exibições
- Última mensagem por Leonardonc

Seg Ago 27, 2012 09:27
Matemática Financeira
-
- demonstração de fórmula
 por Troe » Ter Out 20, 2009 18:07
por Troe » Ter Out 20, 2009 18:07
- 0 Respostas
- 2172 Exibições
- Última mensagem por Troe

Ter Out 20, 2009 18:07
Trigonometria
-
- Qual é a fórmula?
por thales7l » Qua Nov 04, 2009 18:02
- 1 Respostas
- 2223 Exibições
- Última mensagem por Neperiano

Dom Set 18, 2011 13:53
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\left [f_{1}(x).f_{2}(x).\cdot \cdot \cdot f_{N}(x) \right ]=\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\prod_{j=1}^{N}f_{i}(x) = ? \frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\left [f_{1}(x).f_{2}(x).\cdot \cdot \cdot f_{N}(x) \right ]=\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\prod_{j=1}^{N}f_{i}(x) = ?](/latexrender/pictures/7d406c2be6b194be99b00e6387bac8e7.png)

![\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\left [f_{1}(x).f_{2}(x).\cdot \cdot \cdot f_{N}(x) \right ]=\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\prod_{j=1}^{N}f_{i}(x) = ? \frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\left [f_{1}(x).f_{2}(x).\cdot \cdot \cdot f_{N}(x) \right ]=\frac{\mathrm{d}^{n} }{\mathrm{d} x^{n}}\prod_{j=1}^{N}f_{i}(x) = ?](/latexrender/pictures/7d406c2be6b194be99b00e6387bac8e7.png)

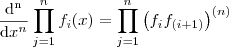 ,onde :
,onde :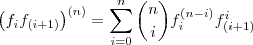


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)