por Higor Yuri » Seg Jun 18, 2012 12:33
por Higor Yuri » Seg Jun 18, 2012 12:33
Consigo achar a equação do plano qndo tenho um ponto e tudo, mas nessa questão me pede pra encontrar os pontos da esfera que é paralalelo a outro plano
Determine os pontos da esfera x²+y²+z²=1 onde o plano tangente é paralelo ao plano 2x + y - 3z = 2
por favor me ajudem
grato
-
Higor Yuri
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 18, 2012 12:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Ter Jun 19, 2012 11:47
por LuizAquino » Ter Jun 19, 2012 11:47
Higor Yuri escreveu:Consigo achar a equação do plano qndo tenho um ponto e tudo, mas nessa questão me pede pra encontrar os pontos da esfera que é paralalelo a outro plano
Determine os pontos da esfera x²+y²+z²=1 onde o plano tangente é paralelo ao plano 2x + y - 3z = 2
Dos conhecimentos de Geometria Analítica, sabemos que dois planos são paralelos quando seus vetores normais possuem a mesma direção (ou seja, os vetores normais são paralelos).
Sabemos que o vetor normal a esfera no ponto

será dado por
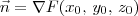
, onde

.
Caculando o gradiente, temos que
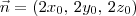
.
Por outro lado, um vetor normal do plano 2x + y - 3z = 2 será dado por
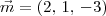
.
Para que os vetores

e
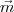
possuam a mesma direção, deve existir um escalar
k tal que
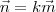
. De onde concluímos que:
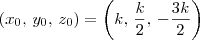
Substituindo essa informação na equação da esfera, temos que:

Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2940 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- PLANO TANGENTE
por renan_cpime14 » Sáb Out 12, 2013 14:49
- 0 Respostas
- 1221 Exibições
- Última mensagem por renan_cpime14

Sáb Out 12, 2013 14:49
Cálculo: Limites, Derivadas e Integrais
-
- Plano tangente
por carolzinhag3 » Seg Abr 10, 2017 23:11
- 2 Respostas
- 2522 Exibições
- Última mensagem por carolzinhag3

Sex Abr 14, 2017 23:46
Cálculo: Limites, Derivadas e Integrais
-
- Equacao plano tangente
por Flames » Ter Mar 13, 2012 00:10
- 4 Respostas
- 2727 Exibições
- Última mensagem por Flames

Ter Mar 13, 2012 23:15
Cálculo: Limites, Derivadas e Integrais
-
- Superfície e Plano Tangente- URGENTE
por leroaquino » Qui Set 17, 2015 19:46
- 2 Respostas
- 2263 Exibições
- Última mensagem por leroaquino

Seg Set 21, 2015 16:10
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 será dado por
será dado por 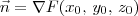 , onde
, onde  .
.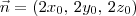 .
.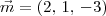 .
. e
e 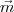 possuam a mesma direção, deve existir um escalar
possuam a mesma direção, deve existir um escalar 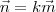 . De onde concluímos que:
. De onde concluímos que: