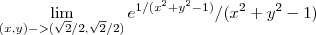 .
.Tentei:
1) Variar x fixando y em 0;
2) Variar y fixando x em 0;
3) Fazer x = y = t.
Mas não consegui fugir da indeterminação.
O limite é 0. Se alguém puder provar, agradeço desde já.

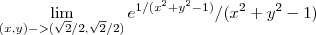 .
.
milerengcomp escreveu:Calcule.
Tentei:
1) Variar x fixando y em 0;
2) Variar y fixando x em 0;
3) Fazer x = y = t.
Mas não consegui fugir da indeterminação.
O limite é 0. Se alguém puder provar, agradeço desde já.
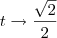 temos que
temos que 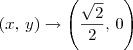 . Note que esse não é o ponto desejado para o limite.
. Note que esse não é o ponto desejado para o limite.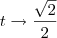 , temos que
, temos que 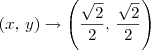 .
.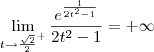
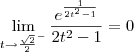
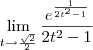 não existe. Como para esse caminho o limite não existe, temos que o limite original também não existe.
não existe. Como para esse caminho o limite não existe, temos que o limite original também não existe.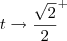 , temos que
, temos que 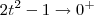 . Sendo assim, teremos que
. Sendo assim, teremos que 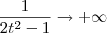 e
e 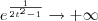 . Usando essas informações, temos que:
. Usando essas informações, temos que: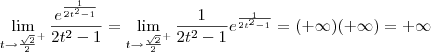
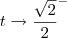 , temos que
, temos que 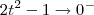 . Sendo assim, teremos que
. Sendo assim, teremos que 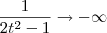 e
e 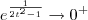 . Usando essas informações, podemos aplicar a Regra de L'Hospital, já que temos uma indeterminação do tipo 0/0. Para facilitar, faremos a substituição
. Usando essas informações, podemos aplicar a Regra de L'Hospital, já que temos uma indeterminação do tipo 0/0. Para facilitar, faremos a substituição 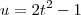 . Temos então que:
. Temos então que: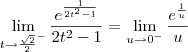
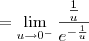
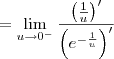
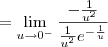
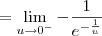
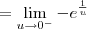

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.