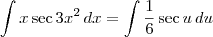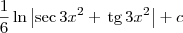por Erick Johnny » Ter Mai 29, 2012 11:01
por Erick Johnny » Ter Mai 29, 2012 11:01
Bom dia srs.
Estou com duvida nesse seguinte exercício:
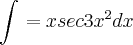
A maneira de fazer essa questão foi por substituição, isolando x do sec3x² ficando:

dai tentei fazer por substituição, chamando sec3x de 'u', sabendo que sua derivada é: sec3x= 3sec3xtg3x. Desenvolvi mas não conseguir resolver a questão. Alguém pode me dar uma luz de como resolver isso?
Atenciosamente
Erick Johnny
-
Erick Johnny
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 29, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por LuizAquino » Ter Mai 29, 2012 12:40
por LuizAquino » Ter Mai 29, 2012 12:40
Erick Johnny escreveu:Estou com duvida nesse seguinte exercício:
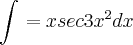
A maneira de fazer essa questão foi por substituição, isolando x do sec3x² ficando:

dai tentei fazer por substituição, chamando sec3x de 'u', sabendo que sua derivada é: sec3x= 3sec3xtg3x. Desenvolvi mas não conseguir resolver a questão. Alguém pode me dar uma luz de como resolver isso?
Você cometeu dois erros
O primeiro erro foi apenas um deslize na digitação. Você deveria ter escrito:
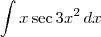
Note que não há aquele "=" que você escreveu.
Já o segundo erro foi mais sério. Você não poderia "isolar o x" da secante como fez. Ou seja,
não é verdade que

.
Por exemplo, se você calcular o valor de

verá que é diferente do valor de

.
Para resolver essa integral, basta fazer a substituição
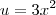
e

(ou seja,
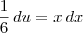
). Nesse caso, temos que:
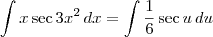
Agora tente concluir o exercício. Se você não conseguir terminar, então poste aqui até onde conseguiu avançar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Erick Johnny » Ter Mai 29, 2012 12:49
por Erick Johnny » Ter Mai 29, 2012 12:49
Obrigado Luiz,
Primeiro pelo erro, não tinha visto o erro de digitação. O segundo erro realmente foi gritante, sabia que saia por substituição mas achava que iria colocar a secante também.
Enfim, gostaria de saber se a resposta final seria:


-
Erick Johnny
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 29, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por LuizAquino » Ter Mai 29, 2012 13:37
por LuizAquino » Ter Mai 29, 2012 13:37
Erick Johnny escreveu:Enfim, gostaria de saber se a resposta final seria:

No Brasil, nós usamos a notação log para representar o logaritmo decimal (ou seja, o logaritmo na base 10). Para representar o logaritmo natural (ou seja, o logaritmo na base e), usamos a notação ln.
Além disso, do jeito que você escreveu note que irá aparecer a constante c/6. Você poderia escrever diferente, de modo a ficar apenas uma constante c.
Em resumo, a resposta adequada seria:
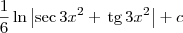
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Ajuda) Duvida no exercício de derivada.
por Kamila conka » Qui Fev 28, 2013 20:41
- 3 Respostas
- 2145 Exibições
- Última mensagem por Kamila conka

Sex Mar 01, 2013 18:32
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DESENVOLVER A DERIVADA TRIGONOMÉTRICA
 por Matheusgdp » Ter Nov 03, 2015 17:34
por Matheusgdp » Ter Nov 03, 2015 17:34
- 5 Respostas
- 3644 Exibições
- Última mensagem por Cleyson007

Sex Nov 06, 2015 08:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivada trigonometrica
por mayara359 » Ter Jun 23, 2015 16:25
- 1 Respostas
- 2511 Exibições
- Última mensagem por Cleyson007

Qua Jun 24, 2015 17:33
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Derivada trigonométrica
por ericamila2 » Sáb Set 24, 2011 22:39
- 1 Respostas
- 1418 Exibições
- Última mensagem por LuizAquino

Sáb Set 24, 2011 23:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de Função Trigonométrica.
por Sobreira » Dom Dez 02, 2012 14:17
- 2 Respostas
- 3536 Exibições
- Última mensagem por MarceloFantini

Seg Dez 03, 2012 00:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
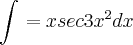



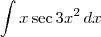
 .
. verá que é diferente do valor de
verá que é diferente do valor de  .
.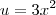 e
e  (ou seja,
(ou seja, 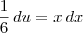 ). Nesse caso, temos que:
). Nesse caso, temos que: