 por will94 » Ter Mai 22, 2012 20:32
por will94 » Ter Mai 22, 2012 20:32
Preciso resolver esse limite, mas não sei como proceder com uma função com duas raízes diferentes:
![\lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right) \lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right)](/latexrender/pictures/983864eef806490ff669accb4c4b8b0d.png)
O resultado eu sei que dá 3.
Muito obrigado àquele(a) que me ajudar.
-
will94
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 22, 2012 20:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Mai 23, 2012 11:46
por LuizAquino » Qua Mai 23, 2012 11:46
will94 escreveu:Preciso resolver esse limite, mas não sei como proceder com uma função com duas raízes diferentes:
![\lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right) \lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right)](/latexrender/pictures/983864eef806490ff669accb4c4b8b0d.png)
O resultado eu sei que dá 3.
Muito obrigado àquele(a) que me ajudar.
Note que:
![\lim_{x\to 64} \frac{\sqrt{x} - 8}{\sqrt[3]{x}-4} = \lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}} \lim_{x\to 64} \frac{\sqrt{x} - 8}{\sqrt[3]{x}-4} = \lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}}](/latexrender/pictures/66270a21122a47c611a833461b2e2428.png)
Agora multiplique o numerador e o denominador pela expressão:
![\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right) \left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)](/latexrender/pictures/dba77f3257add53a39501f628f35dc8a.png)
Temos então que:
![\lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}} = \lim_{x\to 64} \frac{\left(\sqrt{x} - \sqrt{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)}{\left(\sqrt[3]{x}-\sqrt[3]{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)} \lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}} = \lim_{x\to 64} \frac{\left(\sqrt{x} - \sqrt{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)}{\left(\sqrt[3]{x}-\sqrt[3]{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)}](/latexrender/pictures/8748fbeed84caa221b814d6d9b83e8e9.png)
Agora use os seguintes produtos notáveis:
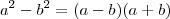
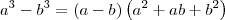
Tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5119 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- limite.como calculo esse limite?
por jeffinps » Ter Mar 12, 2013 12:07
- 1 Respostas
- 2253 Exibições
- Última mensagem por Douglas16

Ter Mar 12, 2013 14:27
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3324 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] calculo de limite trigonométrico
por PRADO » Dom Mai 22, 2016 17:01
- 2 Respostas
- 5623 Exibições
- Última mensagem por PRADO

Sex Jun 03, 2016 23:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Cálculo de limite
por Luciana Bittencourt » Qui Mar 21, 2013 13:10
- 4 Respostas
- 1986 Exibições
- Última mensagem por e8group

Qui Mar 21, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right) \lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right)](/latexrender/pictures/983864eef806490ff669accb4c4b8b0d.png)

![\lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right) \lim_{x\rightarrow 64} \left(\sqrt[2]{x}-8 \right)/\left(\sqrt[3]{x}-4 \right)](/latexrender/pictures/983864eef806490ff669accb4c4b8b0d.png)

![\lim_{x\to 64} \frac{\sqrt{x} - 8}{\sqrt[3]{x}-4} = \lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}} \lim_{x\to 64} \frac{\sqrt{x} - 8}{\sqrt[3]{x}-4} = \lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}}](/latexrender/pictures/66270a21122a47c611a833461b2e2428.png)
![\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right) \left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)](/latexrender/pictures/dba77f3257add53a39501f628f35dc8a.png)
![\lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}} = \lim_{x\to 64} \frac{\left(\sqrt{x} - \sqrt{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)}{\left(\sqrt[3]{x}-\sqrt[3]{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)} \lim_{x\to 64} \frac{\sqrt{x} - \sqrt{64}}{\sqrt[3]{x}-\sqrt[3]{64}} = \lim_{x\to 64} \frac{\left(\sqrt{x} - \sqrt{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)}{\left(\sqrt[3]{x}-\sqrt[3]{64}\right)\left(\sqrt{x} + \sqrt{64}\right)\left(\sqrt[3]{x}^2 + \sqrt[3]{x}\sqrt[3]{64} + \sqrt[3]{64}^2\right)}](/latexrender/pictures/8748fbeed84caa221b814d6d9b83e8e9.png)
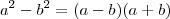
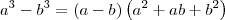

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
