- Mostre que a função
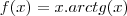 admite inversa no intervalo
admite inversa no intervalo ![(-\infty,0] (-\infty,0]](/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) , e use o Teorema da Função Inversa para calcular
, e use o Teorema da Função Inversa para calcular  .
.
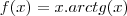 admite inversa no intervalo
admite inversa no intervalo ![(-\infty,0] (-\infty,0]](/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) , e use o Teorema da Função Inversa para calcular
, e use o Teorema da Função Inversa para calcular  .
.
matematicouff escreveu:Como mostro que essa função admite inversa?
- Mostre que a funçãoadmite inversa no intervalo
, e use o Teorema da Função Inversa para calcular
.
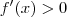 para todo x em [a, b]. Por outro lado, uma função é estritamente decrescente em [a, b] quando
para todo x em [a, b]. Por outro lado, uma função é estritamente decrescente em [a, b] quando 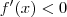 para todo x em [a, b].
para todo x em [a, b].
 .
. ![(-\infty, 0] ==> (-\infty, 0] ==>](/latexrender/pictures/765749b8808879ca2f291b2971349875.png)
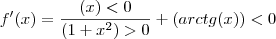 . Logo, f é decrescente nesse intervalo e então admite inversa.
. Logo, f é decrescente nesse intervalo e então admite inversa.
matematicouff escreveu:Ok, derivei a função e deu o seguinte:.
matematicouff escreveu:Analizando o sinal dessa função, vemos que ela é negativa em todo o intervalo![(-\infty, 0] ==> (-\infty, 0] ==>](/latexrender/pictures/765749b8808879ca2f291b2971349875.png)
. Logo, f é decrescente nesse intervalo e então admite inversa.
 .
.![(-\infty,\, 0] (-\infty,\, 0]](/latexrender/pictures/1343a962d509cd11242dfc8c7ae0c7e9.png) .
.matematicouff escreveu:Empaquei agora foi na derivada. Poderia me ajudar?

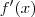 . Basta agora avaliá-la em x = -1.
. Basta agora avaliá-la em x = -1.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)