encontre o valor de A para ser convergente!
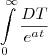
amigos.. ali onde é
 (tendendo ao infinito)
(tendendo ao infinito)eu nao consigo colocar sinal de + na frente.. o correto seria
+

muito obrigado

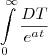
 (tendendo ao infinito)
(tendendo ao infinito)


gabrielnandi escreveu:amigos... me ajudem a solucionar esta questao.
encontre o valor de A para ser convergente!
amigos.. ali onde é(tendendo ao infinito)
eu nao consigo colocar sinal de + na frente.. o correto seria
+
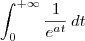
gabrielnandi escreveu:amigos... discupa pedir tudo mastigadinho.. pois eu nao consigo inicia esta questao...
integrate 1/(e^(at)) dt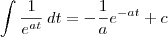
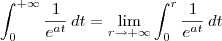
![= \lim_{r\to +\infty} \left[-\frac{1}{a}e^{-at}\right]_0^r = \lim_{r\to +\infty} \left[-\frac{1}{a}e^{-at}\right]_0^r](/latexrender/pictures/2e44c7efc22a5bb862b7aaf53ea08aef.png)
![= \lim_{r\to +\infty} \left[-\frac{1}{a}e^{-ar} - \left(-\frac{1}{a}e^{-a\cdot 0}\right)\right] = \lim_{r\to +\infty} \left[-\frac{1}{a}e^{-ar} - \left(-\frac{1}{a}e^{-a\cdot 0}\right)\right]](/latexrender/pictures/abc90bd9c7ed5917df9a9e2a552fada1.png)
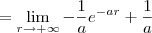
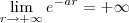 . Por outro lado, sabemos que para a > 0 irá ocorrer
. Por outro lado, sabemos que para a > 0 irá ocorrer  .
.


gabrielnandi escreveu:muito obrigado... mais esses a tem restrições para os valores.. eu imagino que tenha q ser A>0


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

