 por gabriel feron » Seg Mai 14, 2012 16:21
por gabriel feron » Seg Mai 14, 2012 16:21
Boa tarde, gostaria de tirar uma duvida sobre a questao:
![\lim_{x->4}\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} \lim_{x->4}\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}}](/latexrender/pictures/fae81ebb31b82422217342bf0d9a1daf.png)
Nao consigo chegar ao resultado que é
![\frac{2\sqrt[2]{2}}{3} \frac{2\sqrt[2]{2}}{3}](/latexrender/pictures/0917dd4a0286f560a120a1e85caf2d8c.png)
, estou precisando de ajuda para desenvolver a questao, fiz 6 listas de exercicios e só nao consegui chegar ao resultado nessa questão por algum motivo que ainda estou em duvida :S, mas acredito que eu tenha errado na racionalizacao.
Att Gabriel Terra Feron
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 17:54
por LuizAquino » Seg Mai 14, 2012 17:54
gabriel feron escreveu:Boa tarde, gostaria de tirar uma duvida sobre a questao:
![\lim_{x->4}\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} \lim_{x->4}\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}}](/latexrender/pictures/fae81ebb31b82422217342bf0d9a1daf.png)
Nao consigo chegar ao resultado que é
![\frac{2\sqrt[2]{2}}{3} \frac{2\sqrt[2]{2}}{3}](/latexrender/pictures/0917dd4a0286f560a120a1e85caf2d8c.png)
, estou precisando de ajuda para desenvolver a questao, fiz 6 listas de exercicios e só nao consegui chegar ao resultado nessa questão por algum motivo que ainda estou em duvida :S, mas acredito que eu tenha errado na racionalizacao.
Por favor, envie a sua tentativa para que possamos corrigi-la.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por gabriel feron » Seg Mai 14, 2012 18:29
por gabriel feron » Seg Mai 14, 2012 18:29
![\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} vezes \frac{\sqrt[2]{x-2}+\sqrt[2]{2}}{\sqrt[2]{x-2}+\sqrt[2]{2}} = \frac{2x+1-6(\sqrt[2]{2x-1})+9}{x-4}=\frac{2x+10-6^\sqrt[2]{2x-1}}{x-4} \frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} vezes \frac{\sqrt[2]{x-2}+\sqrt[2]{2}}{\sqrt[2]{x-2}+\sqrt[2]{2}} = \frac{2x+1-6(\sqrt[2]{2x-1})+9}{x-4}=\frac{2x+10-6^\sqrt[2]{2x-1}}{x-4}](/latexrender/pictures/d6eede2b87e672066ee06d9368f7b7cb.png)
e agora???
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
 por gabriel feron » Seg Mai 14, 2012 19:05
por gabriel feron » Seg Mai 14, 2012 19:05
Consegui aqui!!!!

Obrigado!!!
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Racionalização
por nathyn » Sex Fev 10, 2012 15:21
- 2 Respostas
- 1553 Exibições
- Última mensagem por nathyn

Seg Fev 13, 2012 12:28
Álgebra Elementar
-
- Racionalização
por Rafael16 » Dom Jan 13, 2013 14:25
- 3 Respostas
- 1814 Exibições
- Última mensagem por Rafael16

Dom Jan 13, 2013 18:41
Aritmética
-
- Racionalização
 por aleson94 » Sex Mai 16, 2014 21:57
por aleson94 » Sex Mai 16, 2014 21:57
- 1 Respostas
- 1412 Exibições
- Última mensagem por Russman

Sex Mai 16, 2014 22:54
Álgebra Elementar
-
- Racionalizaçao
por Gustavo00 » Ter Mai 27, 2014 14:09
- 0 Respostas
- 1155 Exibições
- Última mensagem por Gustavo00

Ter Mai 27, 2014 14:09
Aritmética
-
- Racionalização
por Cristina Lins » Qua Abr 05, 2017 16:52
- 0 Respostas
- 1259 Exibições
- Última mensagem por Cristina Lins

Qua Abr 05, 2017 16:52
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x->4}\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} \lim_{x->4}\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}}](/latexrender/pictures/fae81ebb31b82422217342bf0d9a1daf.png)
![\frac{2\sqrt[2]{2}}{3} \frac{2\sqrt[2]{2}}{3}](/latexrender/pictures/0917dd4a0286f560a120a1e85caf2d8c.png) , estou precisando de ajuda para desenvolver a questao, fiz 6 listas de exercicios e só nao consegui chegar ao resultado nessa questão por algum motivo que ainda estou em duvida :S, mas acredito que eu tenha errado na racionalizacao.
, estou precisando de ajuda para desenvolver a questao, fiz 6 listas de exercicios e só nao consegui chegar ao resultado nessa questão por algum motivo que ainda estou em duvida :S, mas acredito que eu tenha errado na racionalizacao.


![\frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} vezes \frac{\sqrt[2]{x-2}+\sqrt[2]{2}}{\sqrt[2]{x-2}+\sqrt[2]{2}} = \frac{2x+1-6(\sqrt[2]{2x-1})+9}{x-4}=\frac{2x+10-6^\sqrt[2]{2x-1}}{x-4} \frac{\sqrt[2]{2x+1}-3}{\sqrt[2]{x-2}-\sqrt[2]{2}} vezes \frac{\sqrt[2]{x-2}+\sqrt[2]{2}}{\sqrt[2]{x-2}+\sqrt[2]{2}} = \frac{2x+1-6(\sqrt[2]{2x-1})+9}{x-4}=\frac{2x+10-6^\sqrt[2]{2x-1}}{x-4}](/latexrender/pictures/d6eede2b87e672066ee06d9368f7b7cb.png)
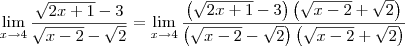
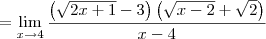
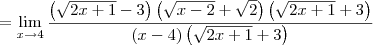
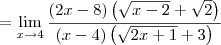
 Obrigado!!!
Obrigado!!! .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.