 por BNK » Sáb Mai 12, 2012 12:32
por BNK » Sáb Mai 12, 2012 12:32
Boas amigos,
Como é possivel determinar um valor aproximado da equação

usando o método de Newton? O exercicio pede isso, só que essa função não tem raiz correto? a derivada da mesma é negativa e supostamente não dá para usar o Método de newton. Mas na solução do exercicio diz que se usou o método de newton e que convergiu à 5ª iteração usando um

. Obtendo-se um valor de x aproximado de 1,2977... Gostava de saber o que me está a escapar nisso!
Obrigado a todos os que puderem ajudar.
-
BNK
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mai 12, 2012 12:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engª Eletrotecnica
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 09:03
por LuizAquino » Seg Mai 14, 2012 09:03
BNK escreveu:Como é possivel determinar um valor aproximado da equação

usando o método de Newton?
Primeiro, isso não é uma
equação, mas sim uma
função.
BNK escreveu:O exercicio pede isso, só que essa função não tem raiz correto?
Correto.
BNK escreveu:a derivada da mesma é negativa e supostamente não dá para usar o Método de Newton.
Errado. Não podemos usar o método quando
f'(
a) = 0, sendo que
a é a raiz de
f(
x) = 0. Note que a derivada pode ser negativa.
BNK escreveu:Mas na solução do exercicio diz que se usou o método de newton e que convergiu à 5ª iteração usando um

. Obtendo-se um valor de x aproximado de 1,2977... Gostava de saber o que me está a escapar nisso!
Qual é o enunciado completo do exercício? Se possível, indique também o local no qual você o encontrou.
Deve haver outra informação no enunciado que você está deixando passar. Do jeito que você escreveu aqui, de fato não faz sentido, já que a função não tem raiz.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por BNK » Seg Mai 14, 2012 17:15
por BNK » Seg Mai 14, 2012 17:15
Olá Luiz,
Obrigado por ter respondido.
Então passo a citar o exercico:
Considere a função
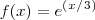
a)Determine io numero de condição f e comente o valor obtido
b)usando o método que achar mais adequado determine um valor aproximado para a raiz da equação

Resp: usando a aproximação inicial

, o metodo de Newton converge à 5ª iteração obtendo-se
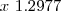
este exercicio foi dado por uma professora pra resolvermos em revisão da matéria
-
BNK
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mai 12, 2012 12:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engª Eletrotecnica
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 17:51
por LuizAquino » Seg Mai 14, 2012 17:51
BNK escreveu:Olá Luiz,
Obrigado por ter respondido.
Então passo a citar o exercico:
Considere a função
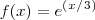
a)Determine io numero de condição f e comente o valor obtido
b)usando o método que achar mais adequado determine um valor aproximado para a raiz da equação

Resp: usando a aproximação inicial

, o metodo de Newton converge à 5ª iteração obtendo-se
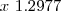
este exercicio foi dado por uma professora pra resolvermos em revisão da matéria
O seu problema foi não saber interpretar o enunciado do exercício.
Note que o enunciado começa dizendo: "
Considere a função 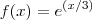
".
Já no quesito b) ele diz: "
determine um valor aproximado para a raiz da equação 
"
Em outras palavras, ele está dizendo para determinar um valor aproximado para a raiz da equação:
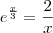
Agora tente continuar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por BNK » Seg Mai 14, 2012 18:02
por BNK » Seg Mai 14, 2012 18:02
LuizAquino escreveu:BNK escreveu:Olá Luiz,
Obrigado por ter respondido.
Então passo a citar o exercico:
Considere a função
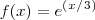
a)Determine io numero de condição f e comente o valor obtido
b)usando o método que achar mais adequado determine um valor aproximado para a raiz da equação

Resp: usando a aproximação inicial

, o metodo de Newton converge à 5ª iteração obtendo-se
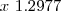
este exercicio foi dado por uma professora pra resolvermos em revisão da matéria
O seu problema foi não saber interpretar o enunciado do exercício.
Note que o enunciado começa dizendo: "
Considere a função 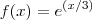
".
Já no quesito b) ele diz: "
determine um valor aproximado para a raiz da equação 
"
Em outras palavras, ele está dizendo para determinar um valor aproximado para a raiz da equação:
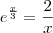
Agora tente continuar o exercício.
Ah booom, é isso, já fiz e deu correto! Muito obrigado!

Já agora, igualei a equação a zero e foi só fazer o método de newton, fácil

. estava mesmo encravado

-
BNK
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mai 12, 2012 12:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engª Eletrotecnica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo numérico, metodo de newton
por Crist » Qua Out 30, 2013 16:47
- 4 Respostas
- 3516 Exibições
- Última mensagem por Crist

Sex Nov 01, 2013 13:46
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Numérico] Método de Newton
por joaofernandes » Dom Jun 19, 2016 19:51
- 0 Respostas
- 1487 Exibições
- Última mensagem por joaofernandes

Dom Jun 19, 2016 19:51
Cálculo: Limites, Derivadas e Integrais
-
- [Método de Newton] - Duvida nessa questão
por zifles2012 » Seg Set 17, 2012 16:13
- 1 Respostas
- 2130 Exibições
- Última mensagem por LuizAquino

Seg Set 17, 2012 19:55
Cálculo Numérico e Aplicações
-
- [método dos pontos críticos] comportamento de uma função
por Ge_dutra » Qua Abr 03, 2013 20:34
- 4 Respostas
- 2854 Exibições
- Última mensagem por Ge_dutra

Qui Abr 04, 2013 20:09
Cálculo: Limites, Derivadas e Integrais
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 8108 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 usando o método de Newton? O exercicio pede isso, só que essa função não tem raiz correto? a derivada da mesma é negativa e supostamente não dá para usar o Método de newton. Mas na solução do exercicio diz que se usou o método de newton e que convergiu à 5ª iteração usando um
usando o método de Newton? O exercicio pede isso, só que essa função não tem raiz correto? a derivada da mesma é negativa e supostamente não dá para usar o Método de newton. Mas na solução do exercicio diz que se usou o método de newton e que convergiu à 5ª iteração usando um  . Obtendo-se um valor de x aproximado de 1,2977... Gostava de saber o que me está a escapar nisso!
. Obtendo-se um valor de x aproximado de 1,2977... Gostava de saber o que me está a escapar nisso!


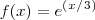
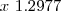
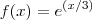
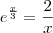




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.