 por kryzay » Seg Mai 14, 2012 09:23
por kryzay » Seg Mai 14, 2012 09:23
Bom dia galera.
Estou estudando derivadas parciais. Porém agora estou com uma dúvida na seguinte função:

Como a função está com exponecial eu não consigo resolve-la.
A professo faz assim:


Semelhante a integração por substituição, ai no du, ela derivada na ordem de apenas uma variável. Ai fica:
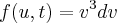

Ai então ela retorna com os valores:
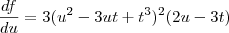
E faz o mesmo com as outras ordens.
Mas está correto isso? Minha dúvida é porque não encontrei material falando de "Derivada por substituição".
Caso não esteja correto, se alguém puder, mostrar a forma correta agradeceria muito.
Bom dia e bons estudos!
-
kryzay
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Jul 25, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 10:40
por LuizAquino » Seg Mai 14, 2012 10:40
kryzay escreveu:Estou estudando derivadas parciais. Porém agora estou com uma dúvida na seguinte função:

Como a função está com exponecial eu não consigo resolve-la.
A professo faz assim:


Semelhante a integração por substituição, ai no du, ela derivada na ordem de apenas uma variável. Ai fica:
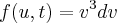

Ai então ela retorna com os valores:
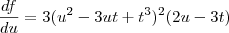
E faz o mesmo com as outras ordens.
Mas está correto isso?
Está correto. Mas eu presumo que ele não escreve
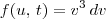
. Provavelmente ele escreve apenas

. O termo dv será escrito apenas na derivada. Ou seja, irá aparecer em
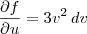
.
kryzay escreveu:Minha dúvida é porque não encontrei material falando de "Derivada por substituição".
Você não deve encontrar coisa alguma com esse nome. Ao invés disso, procure por Regra da Cadeia. Alguns materiais usam essa estratégia de "substituição" ao aplicar essa regra.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por kryzay » Seg Mai 14, 2012 10:58
por kryzay » Seg Mai 14, 2012 10:58
Pode ter sido erro meu ao copiar. Não sei.
Enquanto ao "Derivada por substituição" sabia que não encontraria nada com esse nome.
Agora que sei que posso usar dessa estratégia de substituição, posso continuar com os exercícios.
Novamente muito obrigado Luiz.
Mais uma dúvida resolvida.
-
kryzay
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Jul 25, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:28
- 1 Respostas
- 2264 Exibições
- Última mensagem por adauto martins

Qui Dez 25, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:33
- 1 Respostas
- 1975 Exibições
- Última mensagem por adauto martins

Ter Dez 23, 2014 16:28
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:44
- 2 Respostas
- 2366 Exibições
- Última mensagem por adauto martins

Qua Dez 24, 2014 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Limite de várias variáveis
por braddock » Seg Mai 05, 2014 04:06
- 2 Respostas
- 5029 Exibições
- Última mensagem por braddock

Seg Mai 05, 2014 22:17
Cálculo
-
- [Derivação Implícita] Várias Variáveis
 por Bob90 » Ter Abr 09, 2013 07:52
por Bob90 » Ter Abr 09, 2013 07:52
- 0 Respostas
- 2316 Exibições
- Última mensagem por Bob90

Ter Abr 09, 2013 07:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



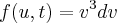

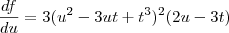


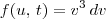 . Provavelmente ele escreve apenas
. Provavelmente ele escreve apenas  . O termo dv será escrito apenas na derivada. Ou seja, irá aparecer em
. O termo dv será escrito apenas na derivada. Ou seja, irá aparecer em 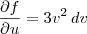 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
