1) Seja
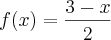 , se x<1; e
, se x<1; e ![f(x)=\frac{1}{\sqrt[]{x}} f(x)=\frac{1}{\sqrt[]{x}}](/latexrender/pictures/7bf247bc7b411982b7b188fef14e9a7b.png) , se x
, se x 1; a)f é diferenciável em x=1? b)f é contínua em x=1?
1; a)f é diferenciável em x=1? b)f é contínua em x=1?Resposta do gabarito: f é diferenciável em x=1 pois f'(1)=-1/2; f é contínua em x=1, pois tem um teorema que garante que toda função diferenciável num ponto é contínua nesse ponto.
2)Seja
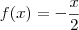 , se x<1; e
, se x<1; e ![f(x)=\frac{1}{\sqrt[]{x}} f(x)=\frac{1}{\sqrt[]{x}}](/latexrender/pictures/7bf247bc7b411982b7b188fef14e9a7b.png) , se x
, se x 1; a)f é diferenciável em x=1? b)f é contínua em x=1?
1; a)f é diferenciável em x=1? b)f é contínua em x=1?Resposta do gabarito:f não é contínua em x=1, pois
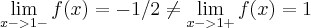 ; f não é diferenciável em x=1 pois se fosse, f seria contínua em x=1.
; f não é diferenciável em x=1 pois se fosse, f seria contínua em x=1.Minha resolução: Na 1ª questão resolvi dessa forma: A função f é diferenciável em x=1 somente se
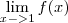 existir.
existir.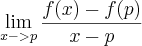 =
= 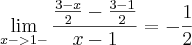 :.
:. ![\lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}=-\frac{1}{2} \lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}=-\frac{1}{2}](/latexrender/pictures/604fef5bfae41462756f094dd03883e6.png) . Como
. Como 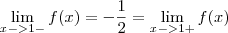 , concluímos que o limite bilateral existe e então podemos dizer que f(x) é derivável em x=1. A função também é contínua em x=1, pois é derivável nesse ponto. Essa minha resposta está de acordo com o gabarito!
, concluímos que o limite bilateral existe e então podemos dizer que f(x) é derivável em x=1. A função também é contínua em x=1, pois é derivável nesse ponto. Essa minha resposta está de acordo com o gabarito!Já a 2ª questão, tentei fazer da mesma forma e deu que
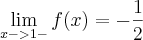 (que está de acordo com o gabarito), mas quando
(que está de acordo com o gabarito), mas quando 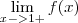 deveria valer -1/2 como na questão anterior, no gabarito diz que vale 1. No que eu errei?
deveria valer -1/2 como na questão anterior, no gabarito diz que vale 1. No que eu errei?

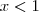 temos que
temos que 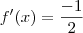 , enquanto que para
, enquanto que para  temos
temos 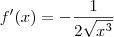 . Calculando os limites laterais, vemos
. Calculando os limites laterais, vemos 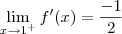 e
e 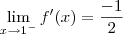 . Como coincidem, o limite existe e a função é diferenciável no ponto, portanto contínua.
. Como coincidem, o limite existe e a função é diferenciável no ponto, portanto contínua.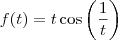 na origem, ou de forma mais extrema procure sobre a
na origem, ou de forma mais extrema procure sobre a 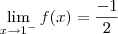 enquanto que
enquanto que 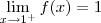 . Como os limites terais são distintos, então a função não é contínua neste ponto, e pelo teorema não é diferenciável.
. Como os limites terais são distintos, então a função não é contínua neste ponto, e pelo teorema não é diferenciável.

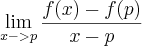
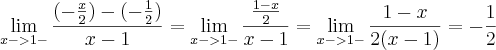
![\lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}= \lim_{x->1+}\frac{\frac{1-\sqrt[]{x}}{\sqrt[]{x}}}{x-1}= \lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}= \lim_{x->1+}\frac{\frac{1-\sqrt[]{x}}{\sqrt[]{x}}}{x-1}=](/latexrender/pictures/c6d5665205758ff973439858642ff8a7.png)
![\lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}= \lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}=](/latexrender/pictures/eeb56b9df0011a388763f8286e646644.png)
![\lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}\frac{(1+\sqrt[]{x})}{(1+\sqrt[]{x})}= \lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}\frac{(1+\sqrt[]{x})}{(1+\sqrt[]{x})}=](/latexrender/pictures/e428fabad833dc0cd9a79867a10aa3c6.png)
![\lim_{x->1+}\frac{1+\sqrt[]{x}-\sqrt[]{x}-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}= \lim_{x->1+}\frac{1+\sqrt[]{x}-\sqrt[]{x}-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}=](/latexrender/pictures/16b4a597a31db09b383e55f593f501d3.png)
![\lim_{x->1+}\frac{1-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}= \lim_{x->1+}\frac{1-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}=](/latexrender/pictures/fd142ad9077de6c2975ee36103bee040.png)
![\lim_{x->1+}-\frac{1}{(\sqrt[]{x})(1+\sqrt[]{x})}= \lim_{x->1+}-\frac{1}{(\sqrt[]{x})(1+\sqrt[]{x})}=](/latexrender/pictures/461ee1846c683cde9462e58ab1e2a624.png)
 .
.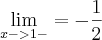 e
e 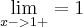 . E como você pode ver nas minhas contas, meus limites laterais deram o mesmo resultado
. E como você pode ver nas minhas contas, meus limites laterais deram o mesmo resultado 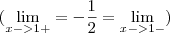

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.