Determine as coordenadas do ponto cuja tangente à curva
 nesse ponto é paralela à secante que passa pelos pontos da curva cujas abcissas são os extremos do intervalo
nesse ponto é paralela à secante que passa pelos pontos da curva cujas abcissas são os extremos do intervalo ![\left[-2, 1 \right] \left[-2, 1 \right]](/latexrender/pictures/88d0463b3c1a50ac9cb82cde912fefc0.png) .
.Passo a explicar a minha resolução:
Primeiro determinei o declive da secante à curva. Para tal, achei as imagens dos pontos da secante (designei por A e por B)
Para A (-2, y1):
y1 = -2 -
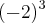 = 6
= 6Para B(1, y2)
y2= 1-1=0
Vetor AB= B-A=(1,0)-(-2,6)= (3,-6), donde m (declive da secante) = -2. Assim, como é paralela à tangente, o declive da tangente também é -2.
Logo, a reta tangente terá de equação y=-2x+b.
A minha dúvida reside aqui: como vou determinar b? Pois não é dado nenhum ponto que pertença à tangente, a não ser o próprio ponto que queremos determinar.




 .
.



