 por ARCS » Qui Mai 03, 2012 01:55
por ARCS » Qui Mai 03, 2012 01:55
Na aula de Mecânica dos Sólidos o professor resolveu o seguinte exercício:
"Uma estaca cravada no solo(
http://imageshack.us/photo/my-images/204/arlan.jpg/) é solicitada por dois trechos de Resultante de Forças Concorrentes corda. Impondo que a resultante das duas forças aplicadas à estaca seja vertical, determine:
a) O valor de alfa para o qual a intensidade de P seja mínima;
b) A correspondente intensidade de P."
Ele resolveu o item a usando a seguinte suposição :"Para que P seja mínima, é necessário que esta seja perpendicular a força de 120N. Com isso chegamos a conclusão que alfa = 65 graus ", e ele mostrou uma animação com Geogebra. Acontece que eu não fiquei conformado com essa resposta e tentei encontra uma uma função usando a lei dos senos e dos cossenos parar em seguida minimiza-la, mas não consegui.
grato desde já
Editado pela última vez por
ARCS em Qui Mai 03, 2012 11:47, em um total de 2 vezes.
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Mai 03, 2012 10:10
por LuizAquino » Qui Mai 03, 2012 10:10
ARCS escreveu:Na aula de Mecânica dos Sólidos o professor resolveu o seguinte exercício:
"
Uma estaca cravada no solo é solicitada por dois trechos de Resultante de Forças Concorrentes corda. Impondo que a resultante das duas forças aplicadas à estaca seja vertical, determine:
a) O valor de alfa para o qual a intensidade de P seja mínima;
b) A correspondente intensidade de P."
Ele resolveu o item a usando a seguinte suposição :"Para que P seja mínima, é necessário que esta seja perpendicular a força de 120N. Com isso chegamos a conclusão que alfa = 65 graus ", e ele mostrou uma animação com Geogebra. Acontece que eu não fiquei conformado com essa resposta e tentei encontra uma uma função usando a lei dos senos e dos cossenos parar em seguida minimiza-la, mas não consegui.
Vamos fixar um sistema de eixos como ilustra a figura abaixo.
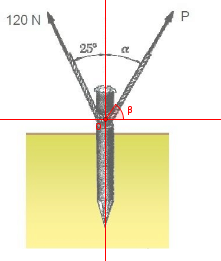
- figura1.png (41.91 KiB) Exibido 3235 vezes
Temos que:
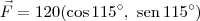

Deseja-se que

seja vertical. Para que isso aconteça, devemos ter:

Desse modo, temos que:
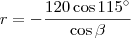
Notando que

, basta determinar

de modo que |r| seja mínimo. Em seguida, note que

é o complementar de

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema de Minimização de Custos
por Fernandobertolaccini » Ter Out 28, 2014 21:54
- 0 Respostas
- 1012 Exibições
- Última mensagem por Fernandobertolaccini

Ter Out 28, 2014 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [Prob. Minimização] Estática
por ARCS » Seg Set 24, 2012 21:36
- 2 Respostas
- 3454 Exibições
- Última mensagem por lucasdemirand

Ter Abr 22, 2014 19:13
Fundamentos de Mecânica
-
- Minimização e zeros um traço de uma matriz
por GoodSpirit » Qui Jan 24, 2013 11:42
- 1 Respostas
- 2192 Exibições
- Última mensagem por GoodSpirit

Sex Jan 25, 2013 13:27
Matrizes e Determinantes
-
- [Minimização de funções] Distância entre duas retas reversas
por guisaulo » Sáb Jun 08, 2013 14:48
- 2 Respostas
- 2592 Exibições
- Última mensagem por guisaulo

Sáb Jun 08, 2013 16:48
Cálculo: Limites, Derivadas e Integrais
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10718 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


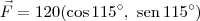

 seja vertical. Para que isso aconteça, devemos ter:
seja vertical. Para que isso aconteça, devemos ter:
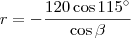
 , basta determinar
, basta determinar  de modo que |r| seja mínimo. Em seguida, note que
de modo que |r| seja mínimo. Em seguida, note que  é o complementar de
é o complementar de 





