 por xanda2012 » Qua Mai 02, 2012 11:30
por xanda2012 » Qua Mai 02, 2012 11:30
Boa dia pessoal, estou com uma dúvida em limites infinitos, é o seguinte:
limite quando x-> infinito negativo de 2x + (raiz) 4x^2 + x ? o que devo fazer para eliminar a raiz e chegar ao resultado? Obrigada

-
xanda2012
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mai 02, 2012 11:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por LuizAquino » Qua Mai 02, 2012 14:31
por LuizAquino » Qua Mai 02, 2012 14:31
xanda2012 escreveu:Boa dia pessoal, estou com uma dúvida em limites infinitos, é o seguinte:
limite quando x-> infinito negativo de 2x + (raiz) 4x^2 + x ? o que devo fazer para eliminar a raiz e chegar ao resultado? Obrigada

Eu presumo que o limite seja:
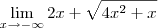
Eu aproveito para pedir que você use o
LaTeX para digitar as notações de forma adequada. Inclusive, isso está nas
Regras do Fórum (vide a regra 2).
Para resolver esse limite, comece multiplicando e dividindo tudo por
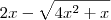
.

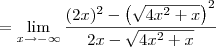

Agora divida o numerador e o denominador por -x.


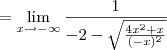
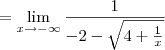

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limites infinitos
por oleve » Qua Jan 21, 2009 18:15
- 1 Respostas
- 3031 Exibições
- Última mensagem por Sandra Piedade

Sáb Jan 24, 2009 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos
por Sobreira » Sáb Out 13, 2012 00:07
- 7 Respostas
- 4540 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 09:07
Cálculo: Limites, Derivadas e Integrais
-
- Limites Infinitos. Ajuda
por valeuleo » Qua Jun 22, 2011 12:39
- 4 Respostas
- 3150 Exibições
- Última mensagem por renatav

Dom Jun 26, 2011 22:46
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos com modulo.
 por Sobreira » Sex Out 12, 2012 18:04
por Sobreira » Sex Out 12, 2012 18:04
- 13 Respostas
- 9069 Exibições
- Última mensagem por Sobreira

Sex Out 12, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos com raiz
por Erick » Sáb Mar 30, 2013 11:11
- 1 Respostas
- 2904 Exibições
- Última mensagem por young_jedi

Sáb Mar 30, 2013 12:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




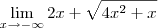
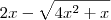 .
.
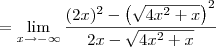



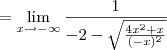
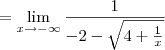


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.