 por Cleyson007 » Sex Abr 27, 2012 12:28
por Cleyson007 » Sex Abr 27, 2012 12:28
Bom dia a todos!
Mostre que se
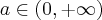
temos
![\lim_{n\rightarrow\infty}\sqrt[n]{n}=1 \lim_{n\rightarrow\infty}\sqrt[n]{n}=1](/latexrender/pictures/09ea436706f0a4c78eeef7cf46024e3e.png)
Se alguém puder me ajudar, agradeço.
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fraol » Sex Abr 27, 2012 13:04
por fraol » Sex Abr 27, 2012 13:04
Bom dia,
Presumo que a expressão seja:
![\lim_{n\rightarrow\infty}\sqrt[n]{a}=1 \lim_{n\rightarrow\infty}\sqrt[n]{a}=1](/latexrender/pictures/f2d63807373e76a086b1b48ea9f175fe.png)
Veja que
![\sqrt[n]{a}=a^{\frac{1}{n}} \sqrt[n]{a}=a^{\frac{1}{n}}](/latexrender/pictures/655383852197bb3f6f0af3a58c0ec0aa.png)
.
O que acontece com o expoente

quando n tende ao infinito?
Veja se consegue prosseguir, do contrário manda a dúvida pra cá.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Cleyson007 » Sáb Abr 28, 2012 10:58
por Cleyson007 » Sáb Abr 28, 2012 10:58
Bom dia Fraol!
Amigo, sinceramente eu não tenho noção de como prosseguir.. Se puder me ajudar com a resolução do exercício ficarei muito grato.
Fico no aguardo.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fraol » Sáb Abr 28, 2012 11:33
por fraol » Sáb Abr 28, 2012 11:33
Bom dia,
Então vamos continuar:
fraol escreveu:O que acontece com o expoente

quando n tende ao infinito?
Vamos atribuir alguns valores crescentes para

e ver como

varia:
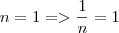



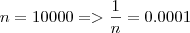
...
Note que ao aumentarmos o valor de n sucessivamente, o valor de

se aproxima cada vez mais de

. Costuma se dizer que a sequência

tende a

quando

tende ao infinito.
Agora aplicando isso ao limite original teremos:
![\lim_{n\rightarrow\infty}\sqrt[n]{a} = \lim_{n\rightarrow\infty} a^{\frac{1}{n}} = a^0 = 1 \lim_{n\rightarrow\infty}\sqrt[n]{a} = \lim_{n\rightarrow\infty} a^{\frac{1}{n}} = a^0 = 1](/latexrender/pictures/5f558d9e8264fb02833c3aa5ea15ee16.png)
.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada - Um Conceito Teórico
por Fabio Cabral » Ter Jun 07, 2011 10:41
- 5 Respostas
- 2826 Exibições
- Última mensagem por MarceloFantini

Ter Jun 07, 2011 12:45
Cálculo: Limites, Derivadas e Integrais
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6558 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11344 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 15298 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 4420 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
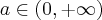 temos
temos ![\lim_{n\rightarrow\infty}\sqrt[n]{n}=1 \lim_{n\rightarrow\infty}\sqrt[n]{n}=1](/latexrender/pictures/09ea436706f0a4c78eeef7cf46024e3e.png)

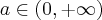 temos
temos ![\lim_{n\rightarrow\infty}\sqrt[n]{n}=1 \lim_{n\rightarrow\infty}\sqrt[n]{n}=1](/latexrender/pictures/09ea436706f0a4c78eeef7cf46024e3e.png)

![\lim_{n\rightarrow\infty}\sqrt[n]{a}=1 \lim_{n\rightarrow\infty}\sqrt[n]{a}=1](/latexrender/pictures/f2d63807373e76a086b1b48ea9f175fe.png)
![\sqrt[n]{a}=a^{\frac{1}{n}} \sqrt[n]{a}=a^{\frac{1}{n}}](/latexrender/pictures/655383852197bb3f6f0af3a58c0ec0aa.png) .
. quando n tende ao infinito?
quando n tende ao infinito?

quando n tende ao infinito?
 e ver como
e ver como  varia:
varia: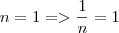



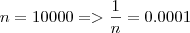
 se aproxima cada vez mais de
se aproxima cada vez mais de  . Costuma se dizer que a sequência
. Costuma se dizer que a sequência  tende a
tende a  quando
quando  tende ao infinito.
tende ao infinito.![\lim_{n\rightarrow\infty}\sqrt[n]{a} = \lim_{n\rightarrow\infty} a^{\frac{1}{n}} = a^0 = 1 \lim_{n\rightarrow\infty}\sqrt[n]{a} = \lim_{n\rightarrow\infty} a^{\frac{1}{n}} = a^0 = 1](/latexrender/pictures/5f558d9e8264fb02833c3aa5ea15ee16.png) .
.
 é uma indeterminação. Mas, observe que supondo:
é uma indeterminação. Mas, observe que supondo: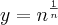

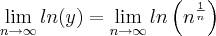

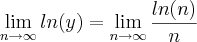
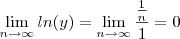
 quando
quando 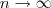 ,
, 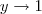 quando
quando 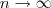 . Dessa forma:
. Dessa forma:![\lim_{n\rightarrow\infty}y = \lim_{n\rightarrow\infty}\sqrt[n]{n}=1 \lim_{n\rightarrow\infty}y = \lim_{n\rightarrow\infty}\sqrt[n]{n}=1](/latexrender/pictures/54e9a991646c2de0edcde39ecf012fc3.png)


 .
.



