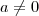por Henrique Bueno » Qui Abr 19, 2012 22:36
por Henrique Bueno » Qui Abr 19, 2012 22:36
Prove que
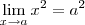
Connsidere separadamente os casos em que a>0 , a<0 e a=0. (considere em sua prova 0<

<a²m quando
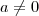
Eu consegui sem problemas fazer a demonstração com a=0, pois qualquer delta e qualquer epsilon irão permitir solucionar, então a solução fica facil... Porém quando se trata do a>0 e a<0 fica mto dificil. Depois de escolher um epsilon não consigo mostrar qual delta usar. Intuitivamente eu pegaria o delta que menos dista do ponto x=a, mas não consigo provar isso.
obrigado pela ajuda
-
Henrique Bueno
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 02, 2011 19:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Abr 19, 2012 23:38
por LuizAquino » Qui Abr 19, 2012 23:38
Henrique Bueno escreveu:Prove que
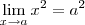
Connsidere separadamente os casos em que a>0 , a<0 e a=0. (considere em sua prova 0<

<a²m quando
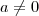
Eu consegui sem problemas fazer a demonstração com a=0, pois qualquer delta e qualquer epsilon irão permitir solucionar, então a solução fica facil... Porém quando se trata do a>0 e a<0 fica mto dificil. Depois de escolher um epsilon não consigo mostrar qual delta usar. Intuitivamente eu pegaria o delta que menos dista do ponto x=a, mas não consigo provar isso.
obrigado pela ajuda
Vide as ideias apontadas nesse tópico:
[Cálculo] Introduçãoviewtopic.php?f=120&t=7723
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Ajuda com demonstração
por ghf » Sex Nov 02, 2012 22:31
- 1 Respostas
- 1481 Exibições
- Última mensagem por MarceloFantini

Sex Nov 02, 2012 22:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limite do produto] Dúvida na demonstração
por BlackSabbathRules » Sex Mai 09, 2014 16:56
- 3 Respostas
- 3036 Exibições
- Última mensagem por e8group

Sáb Mai 10, 2014 15:23
Cálculo: Limites, Derivadas e Integrais
-
- limite: demonstração (acho que utiliza teorema do confronto)
por catabluma123 » Qua Fev 10, 2016 21:52
- 1 Respostas
- 1635 Exibições
- Última mensagem por adauto martins

Seg Fev 22, 2016 12:43
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Demonstração de um limite
por Fabio Marquez » Ter Mai 14, 2013 11:30
- 2 Respostas
- 1699 Exibições
- Última mensagem por Fabio Marquez

Ter Mai 14, 2013 23:55
Cálculo: Limites, Derivadas e Integrais
-
- DEMONSTRAÇÃO
por arima » Seg Nov 08, 2010 08:40
- 8 Respostas
- 5915 Exibições
- Última mensagem por roseli

Qua Nov 10, 2010 21:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
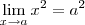
 <a²m quando
<a²m quando