O enunciado é o seguinte: determine a solução do seguinte problema de valor inicial :
![[cos(ln(2y-8))+\frac{1}{x}]dx +\frac{senx}{y-4}dy=0 [cos(ln(2y-8))+\frac{1}{x}]dx +\frac{senx}{y-4}dy=0](/latexrender/pictures/7cac7a88acdd64dcd7c73c2c372a5b77.png) ; y(1)= 9/2.
; y(1)= 9/2.Primeiramente, teremos que provar que é uma equação diferencial exata?
Fiz assim, e segundo os meus cálculos ela não é exata:
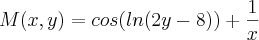 e
e 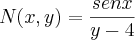 .
.Ora,
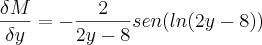 e
e 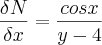 .
.Se não me falha nenhum passo, podemos concluir que não é exata.
Estarei a seguir o caminho correto?
Obrigado!


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)