 por Grasi » Qui Jun 25, 2009 00:12
por Grasi » Qui Jun 25, 2009 00:12
Queremos construir uma lata cilíndrica, de volume 900 ml para servir de embalagem para óleo. Quais devem ser as medidas do raio da base e da altura para que a lata seja a mais econômica possível?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço dede já. Muito obrigada!
-
Grasi
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jun 24, 2009 23:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Qui Jun 25, 2009 11:05
por Molina » Qui Jun 25, 2009 11:05
Grasi escreveu:Queremos construir uma lata cilíndrica, de volume 900 ml para servir de embalagem para óleo. Quais devem ser as medidas do raio da base e da altura para que a lata seja a mais econômica possível?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço dede já. Muito obrigada!
Bom dia, Grasi.
Precisamos minimizar a área superficial da lata, que é dada por:

O volume é dado por
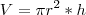
. Ou seja, nesse cado
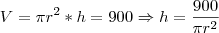
Ou seja, substituindo na equação da área, temos:
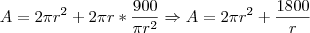
Devemos encontrar o mínimo desta função, logo, derivando A:
![A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}} A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/a8fd927ea03c128e1adfeb175ec60ed3.png)
Fazendo o teste da segunda derivada, temos que
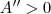
,
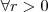
. Com isso
![r=\sqrt[3]{\frac{450}{\pi}} r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/89927c8df6e07acc4435d8e00f189640.png)
é um ponto de mínimo local. Mas o gráfico de A é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.
Conclusão: O raio ideal da base da lata é
![r=\sqrt[3]{\frac{450}{\pi}} r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/89927c8df6e07acc4435d8e00f189640.png)
e a altura ideal dessa lata é
![h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r](/latexrender/pictures/5a6031de7c35462e59c3694417eefa22.png)
Problema grande, porém, se analisar passo a passo verá que não terá grnades problemas.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1992 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:15
- 1 Respostas
- 2550 Exibições
- Última mensagem por Molina

Qui Jun 25, 2009 11:30
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:16
- 1 Respostas
- 2080 Exibições
- Última mensagem por Neperiano

Sáb Set 17, 2011 15:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:18
- 0 Respostas
- 1439 Exibições
- Última mensagem por Grasi

Qui Jun 25, 2009 00:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:20
- 0 Respostas
- 1440 Exibições
- Última mensagem por Grasi

Qui Jun 25, 2009 00:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



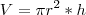 . Ou seja, nesse cado
. Ou seja, nesse cado 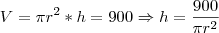
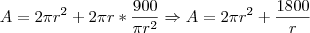
![A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}} A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/a8fd927ea03c128e1adfeb175ec60ed3.png)
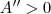 ,
, 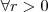 . Com isso
. Com isso ![r=\sqrt[3]{\frac{450}{\pi}} r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/89927c8df6e07acc4435d8e00f189640.png) é um ponto de mínimo local. Mas o gráfico de A é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.
é um ponto de mínimo local. Mas o gráfico de A é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.![h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r](/latexrender/pictures/5a6031de7c35462e59c3694417eefa22.png)

