 por Cleyson007 » Seg Abr 02, 2012 17:05
por Cleyson007 » Seg Abr 02, 2012 17:05
Boa tarde a todos!
Calcule a integral iterada
![\int_{0}^{\sqrt[]{2}}\int_{-\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}y\,dxdy \int_{0}^{\sqrt[]{2}}\int_{-\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}y\,dxdy](/latexrender/pictures/ab722b14de0ff0de00abd8b761aada9c.png)
Iniciei os cálculos, chegando em:
![\int_{0}^{\sqrt[]{2}}2y\,(\sqrt[]{4-2{y}^{2}})\,dy \int_{0}^{\sqrt[]{2}}2y\,(\sqrt[]{4-2{y}^{2}})\,dy](/latexrender/pictures/27dce4927bb7554e12f5c1c91119311c.png)
Se puder detalhar a resolução ao máximo ficarei agradecido.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Seg Abr 02, 2012 19:22
por MarceloFantini » Seg Abr 02, 2012 19:22
Cleyson, agora faça a substituição

, daí
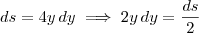
, logo

.
Agora você deve conseguir terminar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral iterada
por JEOVA » Sex Fev 01, 2013 01:45
- 1 Respostas
- 1031 Exibições
- Última mensagem por DanielFerreira

Dom Fev 10, 2013 20:38
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda em Integral Iterada
 por Cleyson007 » Qua Abr 18, 2012 16:50
por Cleyson007 » Qua Abr 18, 2012 16:50
- 1 Respostas
- 832 Exibições
- Última mensagem por DanielFerreira

Qua Abr 18, 2012 21:56
Cálculo: Limites, Derivadas e Integrais
-
- Integral iterada - Região de integração
por Cleyson007 » Sex Abr 13, 2012 23:40
- 9 Respostas
- 4209 Exibições
- Última mensagem por Cleyson007

Dom Abr 15, 2012 18:17
Cálculo: Limites, Derivadas e Integrais
-
- Integral iterada e Região de integração
por Cleyson007 » Sáb Abr 14, 2012 11:21
- 1 Respostas
- 1300 Exibições
- Última mensagem por LuizAquino

Sáb Abr 14, 2012 12:10
Cálculo: Limites, Derivadas e Integrais
-
- Integral iterada e região de integração
por Cleyson007 » Qua Abr 18, 2012 10:59
- 3 Respostas
- 2312 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 23:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{\sqrt[]{2}}\int_{-\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}y\,dxdy \int_{0}^{\sqrt[]{2}}\int_{-\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}y\,dxdy](/latexrender/pictures/ab722b14de0ff0de00abd8b761aada9c.png)
![\int_{0}^{\sqrt[]{2}}2y\,(\sqrt[]{4-2{y}^{2}})\,dy \int_{0}^{\sqrt[]{2}}2y\,(\sqrt[]{4-2{y}^{2}})\,dy](/latexrender/pictures/27dce4927bb7554e12f5c1c91119311c.png)

![\int_{0}^{\sqrt[]{2}}\int_{-\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}y\,dxdy \int_{0}^{\sqrt[]{2}}\int_{-\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}y\,dxdy](/latexrender/pictures/ab722b14de0ff0de00abd8b761aada9c.png)
![\int_{0}^{\sqrt[]{2}}2y\,(\sqrt[]{4-2{y}^{2}})\,dy \int_{0}^{\sqrt[]{2}}2y\,(\sqrt[]{4-2{y}^{2}})\,dy](/latexrender/pictures/27dce4927bb7554e12f5c1c91119311c.png)

 , daí
, daí 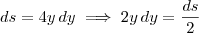 , logo
, logo  .
.
