 por samra » Dom Abr 01, 2012 12:14
por samra » Dom Abr 01, 2012 12:14
Encontrar um intervalo aberto em torno de
a no ql a desigualdade |f(x)-L|<

valha.
Dê então um valor pra

>0 tal que para todo x satisfazendo 0<|x-a|<

a desigualdade |f(x)-L|<seja verdadeira.
f(x)=

, L=3, a=10,

=1
o intervalo eu conseguir achar, da seguinte maneira:
0<|x-10|<


|

-3|<1
3-1<|

<4
2<|

<4
4<|19-x|<16
-15<|-x|<-3
15>|x|>3
logo (3,15) confere com a resposta do livro, acredito que a resolução esteja correta.
Mas ai, o valor de

não consigo achar, sempre acho -7, mas no livro a resposta é 5.
Alguem poderia ajudar-me por favor?
Obg
Ps: Livro Calculo 1, Thomas, pag 92, nro 19
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por fraol » Dom Abr 01, 2012 15:46
por fraol » Dom Abr 01, 2012 15:46
Seu delta deveria ser maior do que 0.
Para

dado, você encontrou
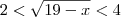
.
Usando esses extremos em
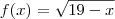
, encontramos

e
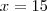
.
Então fixando x em 10, devemos encontrar um

tal que
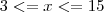
.
Ou seja:
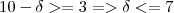
e
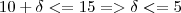
Portanto se você tomar

a implicação do limite será satisfeita.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda para encontrar o "u" na integral
por vmouc » Sex Jun 10, 2011 15:25
- 3 Respostas
- 2419 Exibições
- Última mensagem por vmouc

Sáb Jun 11, 2011 21:05
Cálculo: Limites, Derivadas e Integrais
-
- LEC - encontrar valores
por Washington Murakami » Dom Out 09, 2011 21:55
- 1 Respostas
- 1207 Exibições
- Última mensagem por Washington Murakami

Dom Out 09, 2011 21:59
Matemática Financeira
-
- P.G. (Encontrar os termos)
por Rafael16 » Qua Jul 18, 2012 23:15
- 1 Respostas
- 2504 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 00:02
Progressões
-
- [ PA ] Encontrar termos
por GrazielaSilva » Qui Out 04, 2012 12:42
- 2 Respostas
- 3109 Exibições
- Última mensagem por GrazielaSilva

Sex Out 05, 2012 01:22
Progressões
-
- [ PA ] Encontrar termos
por GrazielaSilva » Qui Out 11, 2012 12:25
- 1 Respostas
- 1674 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 14:08
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 valha.
valha. >0 tal que para todo x satisfazendo 0<|x-a|<
>0 tal que para todo x satisfazendo 0<|x-a|< a desigualdade |f(x)-L|<seja verdadeira.
a desigualdade |f(x)-L|<seja verdadeira. , L=3, a=10,
, L=3, a=10,  =1
=1
 |
| -3|<1
-3|<1 <4
<4 <4
<4 não consigo achar, sempre acho -7, mas no livro a resposta é 5.
não consigo achar, sempre acho -7, mas no livro a resposta é 5.

 dado, você encontrou
dado, você encontrou 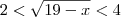 .
.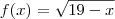 , encontramos
, encontramos  e
e 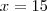 .
.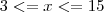 .
.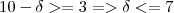 e
e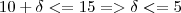
 a implicação do limite será satisfeita.
a implicação do limite será satisfeita.