 por samra » Qui Mar 29, 2012 22:11
por samra » Qui Mar 29, 2012 22:11
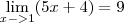
resolvendo fica assim ó:
|f(x)-L|<


0<|x-a|<

|3x+1+5|<

|3x+6|<

3|x+2|<

|x+2|<

0<|x-a|<

portanto:

=

Depois disso, meu professor faz mais alguma coisa que ele chega numa conclusão qe

, e ele disse que só essa forma acima não está totalmente certo, pq ainda não foi provado que o limite existe, pois só é provado qdo

alguem sabe como fazê-lo?
Se sim, coloke o passo a passo com explicação do jeito que eu consiga entender (ainda sou um pouco leiga em limites, principalmente na definição formal)
obg ^^
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por LuizAquino » Sex Mar 30, 2012 19:40
por LuizAquino » Sex Mar 30, 2012 19:40
samra escreveu: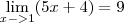
resolvendo fica assim ó:
|f(x)-L|<


0<|x-a|<

|3x+1+5|<

|3x+6|<

3|x+2|<

|x+2|<

0<|x-a|<

portanto:

=

A sua resolução está errada.
Vejamos a definição formal de limite.
Dizemos que
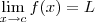
quando temos que: dado

existe

tal que
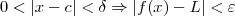
.
No exercício, temos o limite:
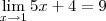
Precisamos então provar que: dado

existe

tal que
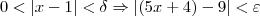
.
Começando pela segunda inequação, temos que:
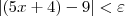

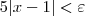
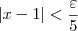
Portanto, na definição formal devemos tomar

. Isto é, dado

fazendo

temos que
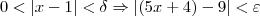
.
Vamos agora verificar que essa escolha de

está correta. Ou seja, vamos verificar que para essa escolha temos que:
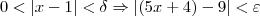
.

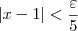
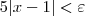

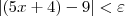
Com isso provamos que:
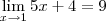
samra escreveu:Depois disso, meu professor faz mais alguma coisa que ele chega numa conclusão qe

, e ele disse que só essa forma acima não está totalmente certo, pq ainda não foi provado que o limite existe, pois só é provado qdo

Você deve estar confundindo a explicação dada. No caso desse exercício que você enviou,
não vamos obter que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por samra » Sex Mar 30, 2012 20:50
por samra » Sex Mar 30, 2012 20:50
Nooh, descupa, eu postei errado o limite

é esse akió

a resolução que eu fiz foi referente ao limite acima :(
se levado em consideração o

minha resolução está certa ou não?

Obrigada!
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por fraol » Sáb Mar 31, 2012 00:16
por fraol » Sáb Mar 31, 2012 00:16
No caso dessa última função que você apresentou, seu

está correto. Contudo, a demonstração deveria seguir o modelo daquela apresentada acima pelo colega LuizAquino.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como se faz essa questão?
por dbarros » Ter Abr 29, 2014 19:04
- 2 Respostas
- 3196 Exibições
- Última mensagem por dbarros

Qua Abr 30, 2014 23:27
Análise Combinatória
-
- como resolver essa questao
por Thassya » Qui Mai 21, 2009 23:25
- 1 Respostas
- 4211 Exibições
- Última mensagem por marciommuniz

Sex Mai 22, 2009 12:23
Trigonometria
-
- Como resolver essa equação?
por viniciusantonio » Qua Out 21, 2009 19:17
- 1 Respostas
- 4151 Exibições
- Última mensagem por carlos r m oliveira

Qui Out 22, 2009 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Como deriva essa equação?
por macburn » Qua Nov 03, 2010 19:14
- 12 Respostas
- 8996 Exibições
- Última mensagem por macburn

Qua Nov 10, 2010 20:36
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo essa equação?
por LuizCarlos » Seg Jul 25, 2011 14:07
- 8 Respostas
- 4946 Exibições
- Última mensagem por LuizCarlos

Ter Jul 26, 2011 00:04
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
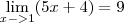

 0<|x-a|<
0<|x-a|<





 =
=
 , e ele disse que só essa forma acima não está totalmente certo, pq ainda não foi provado que o limite existe, pois só é provado qdo
, e ele disse que só essa forma acima não está totalmente certo, pq ainda não foi provado que o limite existe, pois só é provado qdo 


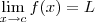 quando temos que: dado
quando temos que: dado  existe
existe  tal que
tal que 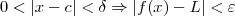 .
.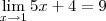
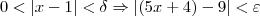 .
.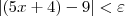

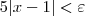
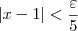
 . Isto é, dado
. Isto é, dado 
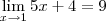
 .
.







 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.