 por Livia000 » Sáb Mar 24, 2012 00:56
por Livia000 » Sáb Mar 24, 2012 00:56
Alguém poderia me ajudar nesta questão?
limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ]
Tentei resolvê-la utilizando a ideia de derivada :
limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ] = limx>1+[ ?(x²-1)/(x+1)/(x-1)] + limx>1+ [ ?(x^3-1)/(x² + x + 1)/(x - 1)] =
limites esses que são iguais às derivadas das funções ?(x²-1)/(x+1) em x= 1 e ?(x^3-1)/( x²+x+1) em x=1 ; respectivamente...
mas, é certo fazer desse jeito, uma vez que não sabemos se o limite de f(x) - f(1)/x-1 qdo x>1 (tende a 1) existe para as duas funções?
*a questão só utiliza o limite pela direita.... o.O
-
Livia000
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Fev 08, 2012 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sáb Mar 24, 2012 11:39
por LuizAquino » Sáb Mar 24, 2012 11:39
Livia000 escreveu:Alguém poderia me ajudar nesta questão?
limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ]
Primeiro, antes de postar um tópico leia as Regras deste fórum:
viewtopic.php?f=9&t=7543Em especial, vide a regra 2.
Livia000 escreveu:limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ]
Tentei resolvê-la utilizando a ideia de derivada :
limx>1+(pela direita) = [ 1/?(x²-1) - 1/?((x^3) - 1) ] = limx>1+[ ?(x²-1)/(x+1)/(x-1)] + limx>1+ [ ?(x^3-1)/(x² + x + 1)/(x - 1)] =
limites esses que são iguais às derivadas das funções ?(x²-1)/(x+1) em x= 1 e ?(x^3-1)/( x²+x+1) em x=1 ; respectivamente...
mas, é certo fazer desse jeito, uma vez que não sabemos se o limite de f(x) - f(1)/x-1 qdo x>1 (tende a 1) existe para as duas funções?
Para qualquer que seja a função real f(x), se 1 é um ponto tal que
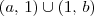
faz parte do domínio de f, então temos que sempre existem os seguintes limites laterais:

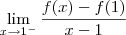
Os resultados desses limites podem ser um número real fixo ou ainda infinito.
Além disso, se os resultados desses dois limites laterais forem distintos, então não existirá o limite "geral":
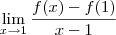
De qualquer modo, não é necessário utilizar o conceito de derivadas nesse exercício. Vejamos a resolução.
Temos o seguinte limite:
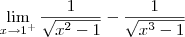
Note que:

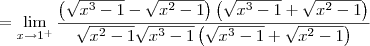

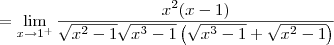

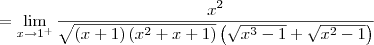
Note que o numerador se aproxima de 1 (pela direita). Já o denominador se aproxima de 0 (pela direita). Desse modo, esse limite é igual a

.
Em resumo, temos então que:
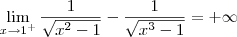
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Livia000 » Sáb Mar 24, 2012 14:30
por Livia000 » Sáb Mar 24, 2012 14:30
Muito obrigada!
Sou novata aqui no fórum, e não conhecia muito bem o latex =) Vou passar a usá-lo a partir de agora.
-
Livia000
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Fev 08, 2012 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4750 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4775 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4803 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2787 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


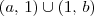 faz parte do domínio de f, então temos que sempre existem os seguintes limites laterais:
faz parte do domínio de f, então temos que sempre existem os seguintes limites laterais:
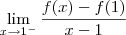
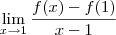
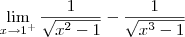

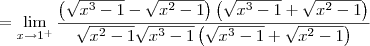

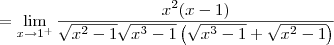

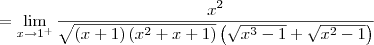
 .
.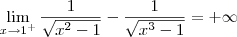



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.