Tenho dúvidas no seguinte exercício:
Calcule a integral dupla, invertendo a ordem de integração:
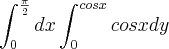 . O resultado indicado no exercício é
. O resultado indicado no exercício é  .
.Comecei a resolver da seguinte forma:
Inverti a ordem, fazendo x= arccos (y) pois y =cos x.
Donde, penso que os novos intervalos de integração ficarão
 . A minha primeira dúvida é se em relação a dy, o intervalo será
. A minha primeira dúvida é se em relação a dy, o intervalo será 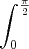 ou será de
ou será de 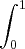 , tendo tem conta a inversão de ordem.
, tendo tem conta a inversão de ordem.No entanto, prossegui a resolução com a ordem invertida
 :
: .
.Procedi à conversão de sen(arccos y) =
![\sqrt[]{(1-{y}^{2})} \sqrt[]{(1-{y}^{2})}](/latexrender/pictures/9dad093d81bd4f3fc322ebd5a1bcff78.png) .
.Donde fiquei com
![\int_{0}^{\frac{\pi}{2}} \sqrt[]{1-{y}^{2}} dy \int_{0}^{\frac{\pi}{2}} \sqrt[]{1-{y}^{2}} dy](/latexrender/pictures/21f274f4a7f097e011a149052f2fc948.png) .
.De seguida, apliquei o método de substituição, onde y=sen (t) e y' = cos (t).
Assim,
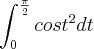 . Surge aqui minha outra dúvida: temos de alterar novamente o intervalo de integração a ordem a t? Ou fica à mesma de 0 a pi/2?
. Surge aqui minha outra dúvida: temos de alterar novamente o intervalo de integração a ordem a t? Ou fica à mesma de 0 a pi/2?Mantendo o intervalo 0 a pi não consigo chegar ao resultado apresentado nas soluções.
Podem-me ajudar?
Obrigado!


 é constante, logo o resultado será
é constante, logo o resultado será 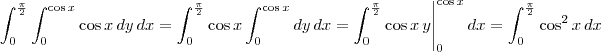 .
.


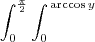 . A minha primeira dúvida é se em relação a dy, o intervalo será
. A minha primeira dúvida é se em relação a dy, o intervalo será  , tendo tem conta a inversão de ordem.
, tendo tem conta a inversão de ordem.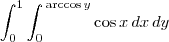
 .
.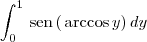
 .
.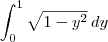
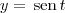 , para y = 0 temos que t = 0. Já para y = 1, temos que t =
, para y = 0 temos que t = 0. Já para y = 1, temos que t =  /2. Portanto, o correto seria:
/2. Portanto, o correto seria: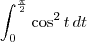
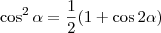 , temos que:
, temos que:
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.