 por panneitz » Sáb Jun 06, 2009 19:43
por panneitz » Sáb Jun 06, 2009 19:43
Não acho meios de solucionar duas questões:
1 - Ache a derivada em relação a x para a função

2 - Ache a área da região limitada pela curva dada: y = x³ - x e y = 0 (eixo x).
Já tentei encontrar a solução na internet, em 5 livros e uma apostila, mas os exemplos e textos não são muito claros.
Peço a gentileza se alguém pode me ajudar, desde já agradeço.
-
panneitz
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 05, 2009 22:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Marcampucio » Sáb Jun 06, 2009 21:26
por Marcampucio » Sáb Jun 06, 2009 21:26
1 - Ache a derivada em relação a x para a função
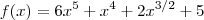
a derivada de uma função polinomial é igual à soma algébrica das derivadas dos têrmos.
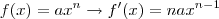
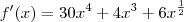
2 - Ache a área da região limitada pela curva dada:
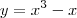
e

(eixo x).
2.1- as raízes de
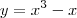
são
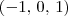
o que significa que ela intercepta o eixo x nesses tres pontos.
2.2-
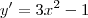
os pontos em que a derivada se anula são os máximos e mínimos da função e temos para
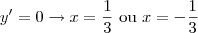
. Temos um máximo em
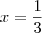
e um mínimo em

. Com esses elementos podemos esboçar o gráfico

a área procurada está destacada em amarelo e é igual a
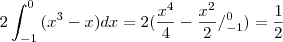
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2261 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7465 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4938 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2962 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1989 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



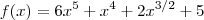
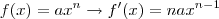
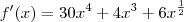
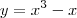 e
e  (eixo x).
(eixo x).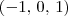 o que significa que ela intercepta o eixo x nesses tres pontos.
o que significa que ela intercepta o eixo x nesses tres pontos.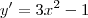 os pontos em que a derivada se anula são os máximos e mínimos da função e temos para
os pontos em que a derivada se anula são os máximos e mínimos da função e temos para 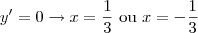 . Temos um máximo em
. Temos um máximo em 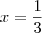 e um mínimo em
e um mínimo em  . Com esses elementos podemos esboçar o gráfico
. Com esses elementos podemos esboçar o gráfico
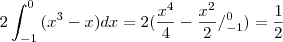



 , avisa que eu resolvo.
, avisa que eu resolvo.

