 por Ana_Rodrigues » Ter Fev 07, 2012 23:43
por Ana_Rodrigues » Ter Fev 07, 2012 23:43
Demonstre que a função:
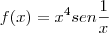
se
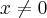
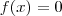
se

é contínua em
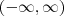
.
Eu não consigo achar continuidade para números acima de zero, por exemplo:
Para x=1 e aplicando o teorema do confronto temos:
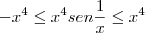
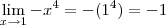
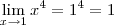
Pelo teorema a função
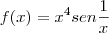
não é contínua para x>0, pois os limites da função não existem quando x>0.
Agradeço desde já, à quem me ajudar a entender!
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Fev 08, 2012 00:12
por LuizAquino » Qua Fev 08, 2012 00:12
Ana_Rodrigues escreveu:Demonstre que a função:
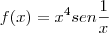
se
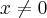
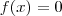
se

é contínua em
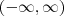
Ana_Rodrigues escreveu:Para x=1 e aplicando o teorema do confronto temos:
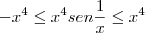
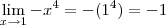
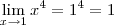
Pelo teorema a função
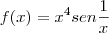
não é contínua para x>0, pois os limites da função não existem quando x>0.
Você está fazendo confusão.
Por definição, para que f seja contínua em x = 1, devemos ter:
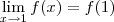
Primeiro, calcule f(1):
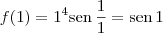
Agora calcule o limite:
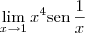
O cálculo desse limite é direto. Note que não há indeterminações.
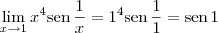
Portanto, temos que
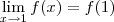
, o que significa que f é contínua em x = 1.
Não há necessidade (e nem faz sentido) aplicar o Teorema do Confronto para esse caso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Ana_Rodrigues » Qua Fev 08, 2012 00:28
por Ana_Rodrigues » Qua Fev 08, 2012 00:28
O Teorema do confronto só serve para indeterminações?
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Fev 08, 2012 00:44
por LuizAquino » Qua Fev 08, 2012 00:44
Ana_Rodrigues escreveu:O Teorema do confronto só serve para indeterminações?
Leia atentamente o enunciado do Teorema do Confronto:
Sejam f(x), g(x) e h(x) funções reais definidas em um domínio
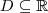
, e seja a, um ponto (finito ou não) deste domínio, tais que:
(i)
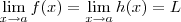
;
(ii)
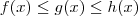
;
Então existe o limite:
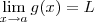
Como
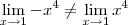
, a afirmação (i) do enunciado do teorema não é atendida. Portanto, não é possível aplicar o teorema nesse caso.
Em resumo: o Teorema do Confronto não ajuda em nada no cálculo de
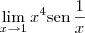
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Demonstrando um limite pela definição
por lucasvier4 » Qui Abr 16, 2015 22:46
- 1 Respostas
- 1525 Exibições
- Última mensagem por adauto martins

Sáb Abr 18, 2015 12:25
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por AlbertoAM » Seg Abr 04, 2011 20:59
- 8 Respostas
- 5659 Exibições
- Última mensagem por LuizAquino

Qua Abr 06, 2011 10:33
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por guilherme5088 » Sáb Out 12, 2019 15:31
- 1 Respostas
- 5324 Exibições
- Última mensagem por adauto martins

Ter Out 15, 2019 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por MCordeiro » Qui Jul 16, 2020 19:11
- 1 Respostas
- 3528 Exibições
- Última mensagem por adauto martins

Qua Out 14, 2020 12:00
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio de Continuidade
por PeIdInHu » Qua Jul 14, 2010 21:04
- 2 Respostas
- 3047 Exibições
- Última mensagem por PeIdInHu

Qui Jul 15, 2010 01:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
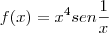 se
se 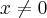
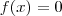 se
se 
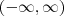 .
.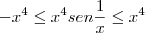
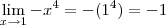
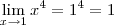
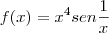 não é contínua para x>0, pois os limites da função não existem quando x>0.
não é contínua para x>0, pois os limites da função não existem quando x>0.

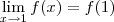
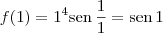
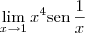
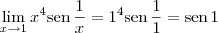

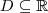 , e seja a, um ponto (finito ou não) deste domínio, tais que:
, e seja a, um ponto (finito ou não) deste domínio, tais que: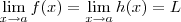 ;
;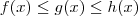 ;
;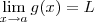
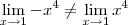 , a afirmação (i) do enunciado do teorema não é atendida. Portanto, não é possível aplicar o teorema nesse caso.
, a afirmação (i) do enunciado do teorema não é atendida. Portanto, não é possível aplicar o teorema nesse caso.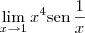 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
