façamos o seguinte... pense na sua piramide posicionada com a base no eixo Oxy e a ponta indo pelo eixo Oz... tudo bem até agora?
agora vamos integrar... quero integrar minúsculas fatias de volume para obter um volume final... Logo, quero:
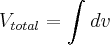
Le-se então: "o volume total é a soma de infinitos pequenos volumes infinitesimais"
(OBS: como pode ver, eu sou estudante de física... os matemáticos provavelmente dirão que eu estou estuprando a matemática... =X mas só estou sendo pratico)
muito simples... agora vamos definir essas tais fatias infinitesimais de volume! quero que voce imagine que estou fatiando a piramide em farias paralelas ao eixo Oxy, tudo bem?
Vou fazer uma simplificação. Pense que, já que são fatias infinitesimalmente pequenas... a figura da fatia, que seria um "tronco de piramide" é, para todos os fins praticos, um paralelepipedo! (matemáticos, respirem fundo, esse é o jeito físico de resolver problemas!)
o que temos então... esse volume infinitesimal que eu estou chamando de dv pode ser escrito em função duma altura infinitesmial, que seria a altura da fatia!!
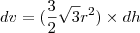
esse R é o tamanho do lado de cada hexagono de cada fatia... é variável conforme as fatias.
perceba que conforme eu vou 'fatiando', conforme cada fatia, esse 'r' muda!
se eu conseguir um jeito de escreve-lo mudando EM FUNÇÂO DE h, eu resolvo o problema!
e é possivel! voce pode, se pensar num corte vertical da piramide, ver que

sendo R e H as medidas dadas no enunciado.
Falta só uma coisa agora... os limites de integração!
eu estou cortando as fatias conforme a altura da piramide! minhas fatias deverão variar de 0 até H... compreende? Vou cortar ao longo da altura, desde o pto 0 até ter completado toda a reta...
(admito que essa explicação pode estar meio acoxambrada, me desculpe, mas fica realmente dificil da-la sem uma lousa =X)
por fim
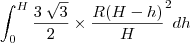
Eis o 'jeito físico' de fazer a matemática...
por favor, desculpe-me de qualquer acoxambramento e qualquer possivel erro =X
Caso algum matemático queira complementar com a resolução mais formal....
obrigado.



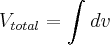
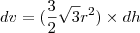

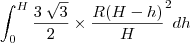





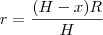
![A = \frac{3\sqrt{3}}{2}\left[\frac{(H-x)R}{H}\right]^2 A = \frac{3\sqrt{3}}{2}\left[\frac{(H-x)R}{H}\right]^2](/latexrender/pictures/640a469a8e976862210315cb960e29f7.png)

![V = \int_0^H \frac{3\sqrt{3}}{2}\left[\frac{(H-x)R}{H}\right]^2\, dx V = \int_0^H \frac{3\sqrt{3}}{2}\left[\frac{(H-x)R}{H}\right]^2\, dx](/latexrender/pictures/21d8940d57a72d9a2a206c83996d56d5.png)
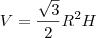


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)