Resolva pela definição de limite a seguinte expressão:
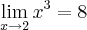
Não entendo a parte que ele faz
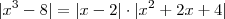 e diz que |x-2|<1.
e diz que |x-2|<1.
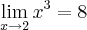
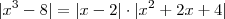 e diz que |x-2|<1.
e diz que |x-2|<1.
Gabriel Doria escreveu:Não estou conseguindo entender a resolução deste seguinte problema se alguém conseguir resolve-lo integralmente seria muito grato.
Resolva pela definição de limite a seguinte expressão:
Não entendo a parte que ele faze diz que |x-2|<1.
 . Isso significa que x é um número cada vez mais próximo de 2. Sendo assim, é razoável dizer, por exemplo, que a distância do número x até o número 2 é menor do que 1 unidade. Ora, mas isso é o mesmo que escrever |x-2|<1.
. Isso significa que x é um número cada vez mais próximo de 2. Sendo assim, é razoável dizer, por exemplo, que a distância do número x até o número 2 é menor do que 1 unidade. Ora, mas isso é o mesmo que escrever |x-2|<1. . Ou seja, podemos dizer nesse caso que
. Ou seja, podemos dizer nesse caso que 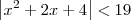 .
.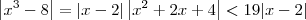
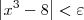 , para um dado
, para um dado  , basta tomar que
, basta tomar que 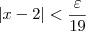 .
. 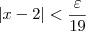 .
. , existe
, existe  , sendo que
, sendo que 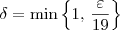 , de tal modo que:
, de tal modo que: 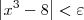 , sempre que
, sempre que  .
.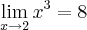 .
.
Continuando a resolução, para |x-2|<1 (que é o mesmo que 1 < x < 3), temos que. Ou seja, podemos dizer nesse caso que
.
Nesse contexto, temos que
Ainda nesse contexto, como devemos ter, para um dado
, basta tomar que
.
Note que até aqui fizemos duas restrições quanto a |x-2|:
(i)|x-2|< 1 ;
(ii).
Portanto, para todo, existe
, sendo que
, de tal modo que:
, sempre que
.
 . Ou seja, podemos dizer nesse caso que
. Ou seja, podemos dizer nesse caso que 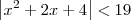 " .
" .
Continuando a resolução, para |x-2|<1 (que é o mesmo que 1 < x < 3), temos que. Ou seja, podemos dizer nesse caso que
.
 , temos que no intervalo [1, 3] ela é crescente (vido o gráfico abaixo). Sendo assim, temos que:
, temos que no intervalo [1, 3] ela é crescente (vido o gráfico abaixo). Sendo assim, temos que:
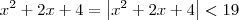

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes