Aliocha Karamazov escreveu:Determine a função cujo gráfico passe pelo ponto (0,1) e tal que a reta tangente no ponto de abscissa x intercepte o eixo Ox no ponto de abscissa x+1.
Aliocha Karamazov escreveu:Seja

a equação da reta tangente ao ponto x do gráfico. Temos que
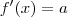
.
Você está confundindo o "x" (fixo) onde avaliar a derivada com o "x" (variável) da equação da reta.
Para não confundir, escreva que a reta tangente a função f no ponto (x, f(x)) é dada por:
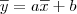
Você sabe que

. Além disso, essa reta deve passar no ponto (x, f(x)). Substituindo então

e
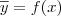
, obtemos que:

Sendo assim, a equação da reta tem o formato:
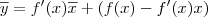
Por outro lado, essa reta corta o eixo Ox no ponto (x+1, 0). Dessa forma, substituindo
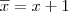
e

, obtemos que:

Note que se a função f é tal que

, então ela tem o formato

(tente obter essa conclusão).
Por fim, usando o fato de que o gráfico de f passa pelo ponto (0, 1), temos que:
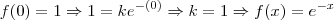
 a equação da reta tangente ao ponto x do gráfico. Temos que
a equação da reta tangente ao ponto x do gráfico. Temos que 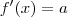 .
.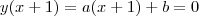 Pois o ponto de abscissa (x+1) corta o eixo Ox.
Pois o ponto de abscissa (x+1) corta o eixo Ox.


 e portanto a reta tangente passando por 0 deve cortando o eixo Ox no ponto de abscissa 1?
e portanto a reta tangente passando por 0 deve cortando o eixo Ox no ponto de abscissa 1?


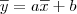
 . Além disso, essa reta deve passar no ponto (x, f(x)). Substituindo então
. Além disso, essa reta deve passar no ponto (x, f(x)). Substituindo então  e
e 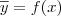 , obtemos que:
, obtemos que:
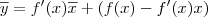
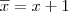 e
e  , obtemos que:
, obtemos que:
 , então ela tem o formato
, então ela tem o formato  (tente obter essa conclusão).
(tente obter essa conclusão).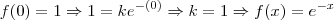
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)