 por procyon » Seg Nov 21, 2011 18:53
por procyon » Seg Nov 21, 2011 18:53
Olá pessoal,
Estou com dúvidas no seguinte exerc?cio:

Tentei fazer o seguinte:
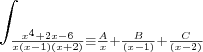
= x²(A + B +C) +x(-3A -2B -C) +2A
2A = -6
A = -3
B = 2
C = 1
=

=
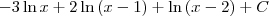
Mas a resposta dá:

A parte do logaritmo está igual mas falta essa parte do x ao quadrado sobre dois - x. Isso deve ser uma primitiva de x (que dá: x^2/2) - primitiva de -1 ( que dá -x). Não sei como isso vai parar no resultado mas acredito que seja algo relacionado ao x na quarta potência que eu ignorei para achar o valor de A, preferi encontrar o A a partir da igualdade com o termo independente do numerador.
Onde está o meu erro?
Obrigado!
-
procyon
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 31, 2011 23:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Nov 21, 2011 20:07
por MarceloFantini » Seg Nov 21, 2011 20:07
Você deve fazer a divisão polinomial para que o grau do numerador seja menor que do denominador, e depois usar frações parciais.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Seg Nov 21, 2011 20:57
por LuizAquino » Seg Nov 21, 2011 20:57
procyon escreveu:Onde está o meu erro?
Como já apontou o colega
Fantini, note que o grau do polinômio no numerador está maior do que o grau do polinômio no denominador.
Eu recomendo que você veja o Exemplo 2 da vídeo aula "29. Cálculo I - Integração por Frações Parciais (Caso I e II)". Ele é semelhante ao exercício que você está resolvendo.
Esta vídeo aula está disponível no meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Integração por frações Parciais
por MCG » Ter Abr 09, 2013 21:03
- 1 Respostas
- 1132 Exibições
- Última mensagem por young_jedi

Qua Abr 10, 2013 15:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por frações racionais] Resposta diferente
por rafiusk » Dom Out 07, 2012 00:44
- 5 Respostas
- 2731 Exibições
- Última mensagem por rafiusk

Seg Out 08, 2012 04:16
Cálculo: Limites, Derivadas e Integrais
-
- [operação com frações simples]
por Aprendiz2012 » Seg Ago 20, 2012 20:07
- 1 Respostas
- 1370 Exibições
- Última mensagem por Cleyson007

Ter Ago 21, 2012 10:23
Equações
-
- [Tecnicas de integraçao por substiuiçao simples]
por menino de ouro » Qua Out 24, 2012 16:12
- 1 Respostas
- 1500 Exibições
- Última mensagem por young_jedi

Qua Out 24, 2012 16:51
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integração por substituiçao - raiz
por beel » Dom Nov 20, 2011 22:33
- 1 Respostas
- 1423 Exibições
- Última mensagem por LuizAquino

Seg Nov 21, 2011 10:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

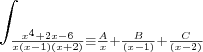

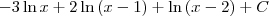





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.