


cassiano07 escreveu:Num primeiro momento a pedra percorreu metade do caminho (1/2) , no outro momento metade da metade (1/4) , posteriormente metade da metade da metade (1/8) e assim continua
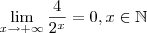
cassiano07 escreveu:até que a pedra colide com a parede que está a 4 metros de distância.

joaofonseca escreveu:Para uma boa resolução de um problema em matematica, um enunciado explicito é essencial.Num primeiro momento a pedra percorreu metade do caminho (1/2) , no outro momento metade da metade (1/4) , posteriormente metade da metade da metade (1/8) e assim continua
Daqui se poderia deduzir o seguinte limite:
joaofonseca escreveu:Ou seja no limite a pedra iria cair na vertical e ficar no mesmo sitio!
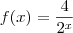 , com
, com 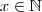 , representa a quantidade que a pedra irá percorrer no tempo x. Essa função não representa a quantidade total percorrida desde a posição inicial da pedra.
, representa a quantidade que a pedra irá percorrer no tempo x. Essa função não representa a quantidade total percorrida desde a posição inicial da pedra.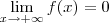 é que para um tempo muito grande, a pedra não irá mais se locomover. Ou seja, ela irá atingir a parede.
é que para um tempo muito grande, a pedra não irá mais se locomover. Ou seja, ela irá atingir a parede.joaofonseca escreveu:até que a pedra colide com a parede que está a 4 metros de distância.
Em que é que ficamos?
Provavelmente o enunciado do problema não está corretamente escrito.

![S_x = \frac{\frac{4}{2}\left[\left(\frac{1}{2}\right)^x - 1\right]}{\frac{1}{2}-1} S_x = \frac{\frac{4}{2}\left[\left(\frac{1}{2}\right)^x - 1\right]}{\frac{1}{2}-1}](/latexrender/pictures/eda547c50460e06cf114deb6ad0db172.png)
![\lim_{x\to+\infty} S_x = \lim_{x\to+\infty} \frac{\frac{4}{2}\left[\left(\frac{1}{2}\right)^x-1\right]}{\frac{1}{2}-1} = \frac{\frac{4}{2}\left(0-1\right)}{\frac{1}{2}-1} = 4 \lim_{x\to+\infty} S_x = \lim_{x\to+\infty} \frac{\frac{4}{2}\left[\left(\frac{1}{2}\right)^x-1\right]}{\frac{1}{2}-1} = \frac{\frac{4}{2}\left(0-1\right)}{\frac{1}{2}-1} = 4](/latexrender/pictures/e1504fea1ad9719f087ee0174ae4c6b4.png)

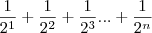 até tender a 0 e atingir a parede. O problema é como provar que o limite é atingido, podendo assim acertar a parede?
até tender a 0 e atingir a parede. O problema é como provar que o limite é atingido, podendo assim acertar a parede?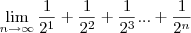 .
.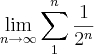 e que quando a razão da Progressão geométrica é <1 , a soma de seus infinitos termos é definida pela fórmula:
e que quando a razão da Progressão geométrica é <1 , a soma de seus infinitos termos é definida pela fórmula:  em que "a1" seria o primeiro termo da progressão e "q" seria a razão.
em que "a1" seria o primeiro termo da progressão e "q" seria a razão.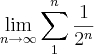 =
= 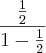 (em que "a1" seja 1/2 e "q" seja 1/2)
(em que "a1" seja 1/2 e "q" seja 1/2)
cassiano07 escreveu:Acho que esse problema é um tipo de paradoxo de Zenão.



LuizAquino escreveu:Portanto, temos que:
 em que "n" é o número de elementos, "q " é a razão e "a1" é o primeiro elemento.
em que "n" é o número de elementos, "q " é a razão e "a1" é o primeiro elemento.
cassiano07 escreveu:Luiz Aquino, o que eu fiz está certo?
cassiano07 escreveu:(...) quando a razão da Progressão geométrica é <1 , a soma de seus infinitos termos é definida pela fórmula:em que "a1" seria o primeiro termo da progressão e "q" seria a razão. (...)
cassiano07 escreveu:Mas essa resolução seria aceita como uma resolução formal, em que se utiliza limites e derivadas? teria como resolver isso com derivada?

cassiano07 escreveu:
A fórmula da soma dos elementos da P.G. não está errada? a que encontrei eraem que "n" é o número de elementos, "q " é a razão e "a1" é o primeiro elemento.
Seria (1- q^n) e não (q^n - 1)?
![\frac{a_1(1-q^n)}{1-q} = \frac{a_1[-(-1+q^n)]}{-(-1+q)} = \frac{-a_1(q^n - 1)}{-(q - 1)} = \frac{a_1(q^n - 1)}{q - 1} \frac{a_1(1-q^n)}{1-q} = \frac{a_1[-(-1+q^n)]}{-(-1+q)} = \frac{-a_1(q^n - 1)}{-(q - 1)} = \frac{a_1(q^n - 1)}{q - 1}](/latexrender/pictures/0b22058a1d864be1880eedf8725c94ab.png)


cassiano07 escreveu:Será que se eu seguir o modo como você fez estará completo? ou devo provar a formula da PG?
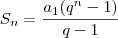 ;
;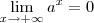 .
.cassiano07 escreveu:Caso deva provar a formula teria como me dar uma ideia?




cassiano07 escreveu:Alguém sabe analisar esse problema pelo método da série convergente? Utilizando algum dos testes de convergência?
 e
e 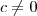 , então
, então 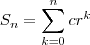 converge para o número
converge para o número 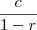 .
.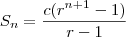 ;
;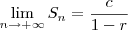 ;
; converge para o número
converge para o número 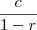 .
.

cassiano07 escreveu:nesse caso o c significaria o a1 e o r a razão?
cassiano07 escreveu:o k representaria o n?

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.