 por Vincent Mazzei » Dom Abr 19, 2009 15:47
por Vincent Mazzei » Dom Abr 19, 2009 15:47
Dado que

encontre, se existir, o limite. Caso não exista, explique por quê.
(só vou colocar uma alternativa)(d)
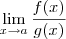
-
Vincent Mazzei
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Abr 19, 2009 15:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por marciommuniz » Dom Abr 19, 2009 16:06
por marciommuniz » Dom Abr 19, 2009 16:06
Pelas propriedades dos limites temos que

Sabemos que não existe divisão por zero, então o limite
não existe!Bons estudos!
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por Vincent Mazzei » Dom Abr 19, 2009 16:38
por Vincent Mazzei » Dom Abr 19, 2009 16:38
Mas e se f(x) for
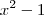
e g(x) for

sabemos que o limite quando x tende a 1 é igual a dois, foi por essa razão que fiquei em dúvida e pensei em responder: "impossível definir sem conhecer as funções". Estou errado?
-
Vincent Mazzei
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Abr 19, 2009 15:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Abr 20, 2009 12:56
por Molina » Seg Abr 20, 2009 12:56
Vincent Mazzei escreveu:Mas e se f(x) for
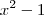
e g(x) for

sabemos que o limite quando x tende a 1 é igual a dois, foi por essa razão que fiquei em dúvida e pensei em responder: "impossível definir sem conhecer as funções". Estou errado?
Vê se é isso que você tinha dúvida:
Considerando as funções que você informou, e fazendo o quociente de uma pela a outra temos que:

Caso não for sua dúvida, desculpa.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4751 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4776 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4806 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2789 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

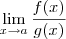


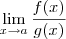



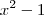 e g(x) for
e g(x) for  sabemos que o limite quando x tende a 1 é igual a dois, foi por essa razão que fiquei em dúvida e pensei em responder: "impossível definir sem conhecer as funções". Estou errado?
sabemos que o limite quando x tende a 1 é igual a dois, foi por essa razão que fiquei em dúvida e pensei em responder: "impossível definir sem conhecer as funções". Estou errado?
e g(x) for
sabemos que o limite quando x tende a 1 é igual a dois, foi por essa razão que fiquei em dúvida e pensei em responder: "impossível definir sem conhecer as funções". Estou errado?





 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.