 por carvalhothg » Seg Set 19, 2011 11:10
por carvalhothg » Seg Set 19, 2011 11:10
- A função definida por

, calcular a derivada da sua função inversa no ponto y=4.
Pessoal eu estou com dificuldades para resolver este exercício, chega uma hora que parece que não tem solução.
Alguém consegue chegar na derivada da função inversa?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Seg Set 19, 2011 11:27
por LuizAquino » Seg Set 19, 2011 11:27
carvalhothg,
Eu recomendo que você assista a vídeo-aula "15. Cálculo I - Derivada da Função Inversa". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoNessa vídeo-aula há um exercício semelhante a esse. Note que se
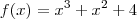
, então o exercício solicita que seja calculado
![\left[f^{-1}(4)\right]^\prime \left[f^{-1}(4)\right]^\prime](/latexrender/pictures/4df208034767e862f83fbb9caad76168.png)
.
Caso a dúvida persista após assistir a vídeo-aula, então poste aqui até onde você conseguiu desenvolver.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carvalhothg » Seg Set 19, 2011 12:08
por carvalhothg » Seg Set 19, 2011 12:08
Prof. Aquino,
sobre o que é derivada inversa eu sei, o problema que parece que não tem solução. Pois olha como que fica:
-onde g(y) é a função inversa de f(x)
y - 4 = g(y).[g(y) + 1]
A duvida é, como isolar g(y) para poder derivar ele. Tem alguma dica?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Seg Set 19, 2011 12:14
por LuizAquino » Seg Set 19, 2011 12:14
carvalhothg escreveu:A duvida é, como isolar g(y) para poder derivar ele. Tem alguma dica?
Você não precisa determinar a função inversa explicitamente para em seguida derivá-la.
Veja a resolução do Exemplo 5 da vídeo-aula acima. A resolução começa a partir dos 8:04 do vídeo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carvalhothg » Seg Set 19, 2011 12:45
por carvalhothg » Seg Set 19, 2011 12:45
Prof. Aquino,
muito obrigado, pois nem no livro que estou utilizando (Calculo A - Diva Flemming) tinha encontrado aquele método de se calcular a derivada inversa de uma função...mais uma vez muito obrigado.
E parabéns por este seu trabalho brilhante.
Abraços.
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Seg Set 19, 2011 16:44
por LuizAquino » Seg Set 19, 2011 16:44
carvalhothg escreveu:muito obrigado, pois nem no livro que estou utilizando (Calculo A - Diva Flemming) tinha encontrado aquele método de se calcular a derivada inversa de uma função...
Bem, eu suponho que você quis dizer: "(...) de se calcular a derivada
da inversa de uma função (...)".
No livro de Cálculo (vol. I) de Hamilton Guidorizzi você pode encontrar o uso desse tipo de estratégia.
carvalhothg escreveu:E parabéns por este seu trabalho brilhante.
Bem, eu acredito que
brilhante é gentileza de sua parte.

De qualquer modo, algo eu posso afirmar: eu procuro fazê-lo o melhor que eu posso.

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Por favor me ajudem
por carvalhothg » Sáb Nov 05, 2011 22:17
- 1 Respostas
- 1295 Exibições
- Última mensagem por LuizAquino

Ter Nov 08, 2011 00:34
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada-gráficos]me ajudem
 por bernardo1744 » Seg Nov 28, 2011 19:34
por bernardo1744 » Seg Nov 28, 2011 19:34
- 3 Respostas
- 1380 Exibições
- Última mensagem por LuizAquino

Ter Nov 29, 2011 10:16
Cálculo: Limites, Derivadas e Integrais
-
- [ Derivada ] Ajudem-me POR FAVOR
por Rendeiro » Dom Fev 19, 2012 18:00
- 5 Respostas
- 2459 Exibições
- Última mensagem por LuizAquino

Seg Fev 20, 2012 12:11
Cálculo: Limites, Derivadas e Integrais
-
- Calculo sem derivada, me ajudem a resolver por favor
por roberta emiliano » Qua Nov 28, 2012 11:54
- 2 Respostas
- 2584 Exibições
- Última mensagem por roberta emiliano

Qua Nov 28, 2012 14:58
Geometria Analítica
-
- [taxa de variação- Derivada] me ajudem nessa questão.
por fabriel » Sex Set 21, 2012 17:59
- 2 Respostas
- 2639 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 00:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , calcular a derivada da sua função inversa no ponto y=4.
, calcular a derivada da sua função inversa no ponto y=4.
 , calcular a derivada da sua função inversa no ponto y=4.
, calcular a derivada da sua função inversa no ponto y=4.
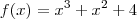 , então o exercício solicita que seja calculado
, então o exercício solicita que seja calculado ![\left[f^{-1}(4)\right]^\prime \left[f^{-1}(4)\right]^\prime](/latexrender/pictures/4df208034767e862f83fbb9caad76168.png) .
.







 .
.



