 por gabrielspadon » Sex Set 16, 2011 11:55
por gabrielspadon » Sex Set 16, 2011 11:55
Como calculo esse limite?
![\lim_{x \to \ 5} \frac {\sqrt[2]{x} - \sqrt[2]{5}}{\sqrt[2]{x+5} - \sqrt[2]{10}} \lim_{x \to \ 5} \frac {\sqrt[2]{x} - \sqrt[2]{5}}{\sqrt[2]{x+5} - \sqrt[2]{10}}](/latexrender/pictures/33d320260681c13aeb06a135b71cc506.png)
-
gabrielspadon
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jul 02, 2011 22:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Aliocha Karamazov » Sex Set 16, 2011 16:38
por Aliocha Karamazov » Sex Set 16, 2011 16:38
Comece multiplicando, no numerador e no denominador, pelos conjugados de ambos.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Anne2011 » Sex Set 16, 2011 17:27
por Anne2011 » Sex Set 16, 2011 17:27
O -5 da segunda equação não é expoente, não estou muito familiarizada com o látex...

-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 17:36
por MarceloFantini » Sex Set 16, 2011 17:36
Anne, isto que você fez está errado, não faz sentido e não é a dica de Aliocha. Multiplique numerador e denominador por

, faça algumas distributivas e veja o que acontece.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Anne2011 » Sex Set 16, 2011 17:57
por Anne2011 » Sex Set 16, 2011 17:57
Ops, tens razão... Pera q vou tentar de novo...
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por Anne2011 » Sex Set 16, 2011 18:22
por Anne2011 » Sex Set 16, 2011 18:22
Fiz aqui e deu indeterminação... Calculo o slimites laterais? (não lembro mais

)
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Anne2011 » Sex Set 16, 2011 18:40
por Anne2011 » Sex Set 16, 2011 18:40
Fantini, agora fiz assim:
![\lim_{x\rightarrow5}\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)}-\sqrt[2]{10}} \lim_{x\rightarrow5}\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)}-\sqrt[2]{10}}](/latexrender/pictures/53196ceef3b567a29edc555c018fa858.png)
![\lim_{x\rightarrow5}{\left(\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)-\sqrt[2]{10}}} \right)}^{2}.{\left(\frac{\sqrt[2]{(x+5)+\sqrt[2]{10}}}{\sqrt[2]{(x+5)+\sqrt[2]{10}}} \right)}^{2} \lim_{x\rightarrow5}{\left(\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)-\sqrt[2]{10}}} \right)}^{2}.{\left(\frac{\sqrt[2]{(x+5)+\sqrt[2]{10}}}{\sqrt[2]{(x+5)+\sqrt[2]{10}}} \right)}^{2}](/latexrender/pictures/2416c2ff4529a40b16f124a2485718a4.png)
Agora sim, cortando as raizes fica:
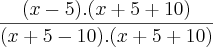
=

E agora?
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por Anne2011 » Sex Set 16, 2011 18:43
por Anne2011 » Sex Set 16, 2011 18:43
Hunm... Tô vendo que terei que rever essa materia...

-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 18:44
por MarceloFantini » Sex Set 16, 2011 18:44
O que você fez está errado no sentido de que você calculou para outra função (e errado também). Verifique minha resolução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Anne2011 » Sex Set 16, 2011 18:59
por Anne2011 » Sex Set 16, 2011 18:59
Ok.

-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por LuizAquino » Sáb Set 17, 2011 10:39
por LuizAquino » Sáb Set 17, 2011 10:39
Anne2011 escreveu:Hunm... Tô vendo que terei que rever essa materia...

Se precisar, então veja se as vídeo-aulas em meu canal podem lhe ajudar:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Anne2011 » Sáb Set 17, 2011 15:01
por Anne2011 » Sáb Set 17, 2011 15:01
Tenho tds os seus vídeos... me ajudando sempre

Agora to vendo os de integrais, tenho prova essa semana e tô apanhando muito pra resolver...
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por gabrielspadon » Sáb Set 17, 2011 19:04
por gabrielspadon » Sáb Set 17, 2011 19:04
Marcelo Fantini, na sua resolução, porque você não aplicou a distributiva tambem na ultima expressão? E porque o sinal das expressões se inverteram?
-
gabrielspadon
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jul 02, 2011 22:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sáb Set 17, 2011 19:26
por MarceloFantini » Sáb Set 17, 2011 19:26
Não apliquei a distributiva pois não era conveniente. Não me ajudaria a perceber que fator se cancelaria, e pelo jeito que a questão foi formulada estava claro que precisava fazer aparecer

no numerador e denominador para cancelar. Que sinal se inverteu? Lembre-se do produto notável

. Neste caso, no numerador por exemplo temos

e
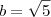
, e assim
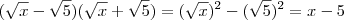
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7256 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4433 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \to \ 5} \frac {\sqrt[2]{x} - \sqrt[2]{5}}{\sqrt[2]{x+5} - \sqrt[2]{10}} \lim_{x \to \ 5} \frac {\sqrt[2]{x} - \sqrt[2]{5}}{\sqrt[2]{x+5} - \sqrt[2]{10}}](/latexrender/pictures/33d320260681c13aeb06a135b71cc506.png)


![\lim_{x \to \ 5} \frac {\sqrt[2]{x} - \sqrt[2]{5}}{\sqrt[2]{x+5} - \sqrt[2]{10}} \lim_{x \to \ 5} \frac {\sqrt[2]{x} - \sqrt[2]{5}}{\sqrt[2]{x+5} - \sqrt[2]{10}}](/latexrender/pictures/33d320260681c13aeb06a135b71cc506.png)


![\lim_{x\rightarrow5}\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{x+5}-\sqrt[2]{10}} \lim_{x\rightarrow5}\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{x+5}-\sqrt[2]{10}}](/latexrender/pictures/c81a7278992eaba218916c87e6d915f7.png)





 , faça algumas distributivas e veja o que acontece.
, faça algumas distributivas e veja o que acontece.


 )
)

![\lim_{x\rightarrow5}\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)}-\sqrt[2]{10}} \lim_{x\rightarrow5}\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)}-\sqrt[2]{10}}](/latexrender/pictures/53196ceef3b567a29edc555c018fa858.png)
![\lim_{x\rightarrow5}{\left(\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)-\sqrt[2]{10}}} \right)}^{2}.{\left(\frac{\sqrt[2]{(x+5)+\sqrt[2]{10}}}{\sqrt[2]{(x+5)+\sqrt[2]{10}}} \right)}^{2} \lim_{x\rightarrow5}{\left(\frac{\sqrt[2]{x}-\sqrt[2]{5}}{\sqrt[2]{(x+5)-\sqrt[2]{10}}} \right)}^{2}.{\left(\frac{\sqrt[2]{(x+5)+\sqrt[2]{10}}}{\sqrt[2]{(x+5)+\sqrt[2]{10}}} \right)}^{2}](/latexrender/pictures/2416c2ff4529a40b16f124a2485718a4.png)
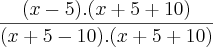 =
=







 Agora to vendo os de integrais, tenho prova essa semana e tô apanhando muito pra resolver...
Agora to vendo os de integrais, tenho prova essa semana e tô apanhando muito pra resolver...




 no numerador e denominador para cancelar. Que sinal se inverteu? Lembre-se do produto notável
no numerador e denominador para cancelar. Que sinal se inverteu? Lembre-se do produto notável  . Neste caso, no numerador por exemplo temos
. Neste caso, no numerador por exemplo temos  e
e 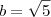 , e assim
, e assim 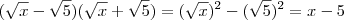 .
.


 .
.
 :
: