Estou começando a aprender derivadas, e travei nisso! tenho que usar log neperiano? quebrei a cabeça mas nao resolvi!
como saio disso?





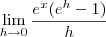

 .
. .
.

vinik1 escreveu:me desculpe, mas não intendi.. (N)
O que seria aparecer o "limite fundamental"?
vinik1 escreveu:Vou assistir a aula e ver se consigo entender
vinik1 escreveu:Joguei esse calculo no Microsoft Mathematics, e a saida foi e^x
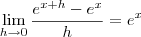
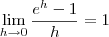

Note que com as informações dadas anteriormente, você deve obter que:

vinik1 escreveu:como?
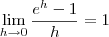
 , temos que
, temos que 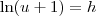 . Além disso, quando
. Além disso, quando 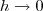 temos que
temos que 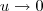 . Desse modo, podemos reescrever o limite como:
. Desse modo, podemos reescrever o limite como: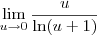




Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
