 por flima » Sáb Ago 27, 2011 14:57
por flima » Sáb Ago 27, 2011 14:57
Olá para todos,
Segue o enunciado:
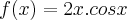
, qual o valor de
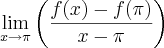
Resposta: -2
Eu tentei substituir

por
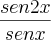
e desenvolver a equação, mas não rolou! Voiltando ao problema inicial, imaginei que a saída era encontrar um fator de evidência para o numerador que fosse igual ao denominador

, assim excluo o zero quando aplicar o limite. O problema é que tentei muita coisa e não consegui. Alguém pode ajudar?

-
flima
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Ago 27, 2011 14:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: engenharia quimica
- Andamento: formado
 por LuizAquino » Sáb Ago 27, 2011 17:34
por LuizAquino » Sáb Ago 27, 2011 17:34
DicaSome e subtraia a expressão

no numerador:

Em seguida, separe em dois limites:

Agora tente terminar de resolver o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Caradoc » Sáb Ago 27, 2011 18:22
por Caradoc » Sáb Ago 27, 2011 18:22
Como é uma indeterminação do tipo 0/0, você também pode tentar usar a regra de L'Hopital.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por flima » Sáb Ago 27, 2011 18:23
por flima » Sáb Ago 27, 2011 18:23
Ai que bom, agora foi!!!! Obrigada.
-
flima
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Ago 27, 2011 14:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: engenharia quimica
- Andamento: formado
 por LuizAquino » Sáb Ago 27, 2011 20:04
por LuizAquino » Sáb Ago 27, 2011 20:04
Caradoc escreveu:Como é uma indeterminação do tipo 0/0, você também pode tentar usar a regra de L'Hopital.
O uso indiscriminado da Regra de L'Hospital pode "enferrujar" a capacidade de manipulação algébrica do estudante.
Por isso, é bom deixar essa regra para os casos específicos nos quais uma manipulação algébrica "elementar" não resolve o limite.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por VtinxD » Dom Ago 28, 2011 03:17
por VtinxD » Dom Ago 28, 2011 03:17
Perceba que isto é uma derivada no ponto

da função f(x),aplicando uma mudança de variavel

para ficar na forma mais convencional ou até olhando como

.E percebendo isto é só usar a regra do produto e avaliar no ponto

-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por LuizAquino » Dom Ago 28, 2011 11:36
por LuizAquino » Dom Ago 28, 2011 11:36
VtinxD escreveu:Perceba que isto é uma derivada no ponto

da função f(x),aplicando uma mudança de variavel

para ficar na forma mais convencional ou até olhando como

.E percebendo isto é só usar a regra do produto e avaliar no ponto

Bem, isso só pode ser feito se já tivesse sido estudado o conceito de derivadas e suas regras operatórias. Mas, o que fazer se não houvesse esse estudo? Perceba que nem essas regras e nem a Regra de L'Hospital poderiam ser aplicadas.
Veja que esse exercício poderia estar perfeitamente na seção de um livro que falasse apenas sobre limite (muito antes de falar sobre derivada, por exemplo).
Nesse contexto, é fundamental saber manipular algebricamente o limite para poder resolvê-lo, sem necessidade de usar de alguma forma o conceito de derivada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mais um limite
por Psilocybe » Ter Mai 31, 2011 20:33
- 2 Respostas
- 1282 Exibições
- Última mensagem por carlosalesouza

Qua Jun 01, 2011 00:27
Cálculo: Limites, Derivadas e Integrais
-
- Mais uma de sequência
por Molina » Dom Mai 03, 2009 06:07
- 4 Respostas
- 2897 Exibições
- Última mensagem por lucasguedes

Ter Jul 07, 2009 21:08
Desafios Difíceis
-
- MAIS UMA QUESTÃO DE G.A
por GABRIELA » Ter Set 29, 2009 18:57
- 3 Respostas
- 2541 Exibições
- Última mensagem por Elcioschin

Qua Set 30, 2009 20:54
Geometria Analítica
-
- Mais uma questão
por GABRIELA » Seg Dez 07, 2009 17:16
- 1 Respostas
- 2192 Exibições
- Última mensagem por Elcioschin

Seg Dez 07, 2009 19:23
Estatística
-
- Mais um desafio..
por victoreis1 » Seg Nov 22, 2010 21:26
- 3 Respostas
- 2522 Exibições
- Última mensagem por Molina

Seg Nov 22, 2010 23:54
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
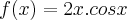 , qual o valor de
, qual o valor de 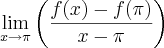
 por
por 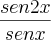 e desenvolver a equação, mas não rolou! Voiltando ao problema inicial, imaginei que a saída era encontrar um fator de evidência para o numerador que fosse igual ao denominador
e desenvolver a equação, mas não rolou! Voiltando ao problema inicial, imaginei que a saída era encontrar um fator de evidência para o numerador que fosse igual ao denominador  , assim excluo o zero quando aplicar o limite. O problema é que tentei muita coisa e não consegui. Alguém pode ajudar?
, assim excluo o zero quando aplicar o limite. O problema é que tentei muita coisa e não consegui. Alguém pode ajudar? 


 no numerador:
no numerador:



 da função f(x),aplicando uma mudança de variavel
da função f(x),aplicando uma mudança de variavel  para ficar na forma mais convencional ou até olhando como
para ficar na forma mais convencional ou até olhando como  .E percebendo isto é só usar a regra do produto e avaliar no ponto
.E percebendo isto é só usar a regra do produto e avaliar no ponto 


 , avisa que eu resolvo.
, avisa que eu resolvo.

