 por 380625 » Qua Ago 17, 2011 18:15
por 380625 » Qua Ago 17, 2011 18:15
Estou estudando o conceito de bola aberta e não consigo entender o que é um ponto interior a uma bola aberta.
Desculpa pela pouca informação pois estou muito confuso.
Grato
Flávio Santana.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Qua Ago 17, 2011 20:41
por MarceloFantini » Qua Ago 17, 2011 20:41
Qual a sua dúvida, especificamente? Talvez algum exercício ou definição que não tenha ficado clara. Soa como se você estivesse confundindo conceitos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por marciosouza » Dom Abr 14, 2013 17:41
por marciosouza » Dom Abr 14, 2013 17:41
PONTO INTERIOR, segue da definição de que:
Def. Seja A(contido em)M e A(diferente de vazio). dizemos que um ponto x é interior de A, se existir uma bola aberta centrada em x e contida em A, de modo que:
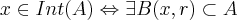
Como exemplo:
Considere em R2 o conjunto dos pontos interiores à uma circunferência de centro (1,1)... todos os pontos internos à circunferência compõe a B(x,1) aberta ***já que os pontos sobre a circunferência pertencem à ela mas não são internos à mesma.
-
marciosouza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Set 20, 2011 16:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Espaços Vetoriais e Espaço Euclidiano.
por 380625 » Dom Ago 14, 2011 16:06
- 1 Respostas
- 1547 Exibições
- Última mensagem por LuizAquino

Dom Ago 14, 2011 16:25
Geometria Analítica
-
- Topologia
por Jadiel Carlos » Qua Nov 23, 2016 01:16
- 4 Respostas
- 3667 Exibições
- Última mensagem por Jadiel Carlos

Qui Nov 24, 2016 13:23
Cálculo: Limites, Derivadas e Integrais
-
- QUESTÃO DE TOPOLOGIA
por marciosouza » Dom Abr 14, 2013 17:28
- 0 Respostas
- 925 Exibições
- Última mensagem por marciosouza

Dom Abr 14, 2013 17:28
Álgebra Elementar
-
- Produto Interno Euclidiano
por ARCS » Sáb Dez 10, 2011 17:57
- 1 Respostas
- 2091 Exibições
- Última mensagem por MarceloFantini

Dom Dez 11, 2011 04:06
Geometria Analítica
-
- dificudade com produto interno euclidiano
por nandooliver008 » Dom Nov 02, 2014 22:29
- 5 Respostas
- 3048 Exibições
- Última mensagem por Russman

Seg Nov 03, 2014 14:46
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





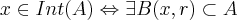

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
