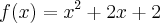determinar o ângulo formado pela reta tangente à uma curva.

[theSinister]

vamos considerar a seguinte função : , e queremos encontrar a inclinação da reta tangente a curva no ponto (1,5), ou seja nada mais do q derivar a função , q ficaria 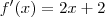, dai substituímos "x "por "1" e encontramos a inclinação de "4". A partir daí fazemos a equação da reta q ficaria 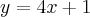, agora a duvida é: como encontrar o ângulo formado entre a reta e o eixo x? Eu sei q o valor desse ângulo é de 75,9 e a tangente dele é 4, porém não entendi como o meu professor encontrou o valor do angulo . help-me.

[LuizAquino]

Você precisa usar a função arco tangente, que é a inversa da função tangente.

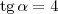Você tem que . Usando uma calculadora científica, obtemos que .

Observação

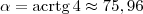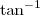1) É comum nas calculadoras científicas aparecer a notação para representar o arco tangente. Portanto, nessas calculadoras você deve digitar .

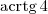2) Sem o uso de calculadora, teríamos que apelar para algum método numérico para calcular . Por exemplo, o Método de Newton. Vale lembrar que esses métodos numéricos são estudados na disciplina Cálculo Numérico.