 por pinkfluor » Qui Jul 21, 2011 11:38
por pinkfluor » Qui Jul 21, 2011 11:38
CONCURSO PETROBRAS 2011:
O grafico abaixo mostra,parcialmente, o grafico da funcao f(x), definida por f(x)= (3x^2)/ (x³+1)
Qual o valor da area limitada pela curva do grafico f, pelo eixo das abscissas e pelas retas x=1 e x=3?
PS. A figura do grafico mostra que a funcao f(x) é positiva no intervalo [1,3].
Gabarito: ln(14)
-
pinkfluor
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 01, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por pinkfluor » Qui Jul 21, 2011 11:43
por pinkfluor » Qui Jul 21, 2011 11:43
pinkfluor escreveu:CONCURSO PETROBRAS 2011:
O grafico abaixo mostra,parcialmente, o grafico da funcao f(x), definida por f(x)= (3x^2)/ (x³+1)
Qual o valor da area limitada pela curva do grafico f, pelo eixo das abscissas e pelas retas x=1 e x=3?
PS. A figura do grafico mostra que a funcao f(x) é positiva no intervalo [1,3].
Gabarito: ln(14)
Entao:
A = integral f(x) dx
Mas pra integrar essa funcao, tenho que fazer fracoes parciais, mas nao tou conseguindo fatorar o denominador (x³+1).
Sabemos que (x³+1) = (x +1)*(x2 - x +1), mas se fatorar essa equacao do segundo grau, nao ha raizes reais...
Alguem sabe???
Obrigada!
-
pinkfluor
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 01, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por MarceloFantini » Qui Jul 21, 2011 14:32
por MarceloFantini » Qui Jul 21, 2011 14:32
Não é necessário fazer frações parciais. Faça a substituição
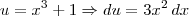
, e portanto a integral será

, basta colocar os limites de integração. Note que quando fazemos mudança de variável é necessário alterar os limites para que o valor final não se altere.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por pinkfluor » Qui Jul 21, 2011 17:21
por pinkfluor » Qui Jul 21, 2011 17:21
MarceloFantini escreveu:Não é necessário fazer frações parciais. Faça a substituição
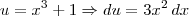
, e portanto a integral será

, basta colocar os limites de integração. Note que quando fazemos mudança de variável é necessário alterar os limites para que o valor final não se altere.
Nossaaa!!nao "enxerguei" que saia por susbstituicao de jeito nenhum...brigadao mesmoooooo!!
sds
-
pinkfluor
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 01, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral - Cálculo de áreas
 por AlbertoAM » Ter Jun 28, 2011 00:25
por AlbertoAM » Ter Jun 28, 2011 00:25
- 5 Respostas
- 6584 Exibições
- Última mensagem por AlbertoAM

Qua Jun 29, 2011 20:44
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Cálculo de Áreas - Guidorizzi
por Lennon » Sáb Jun 08, 2013 02:24
- 2 Respostas
- 2826 Exibições
- Última mensagem por Lennon

Dom Jun 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo de Áreas com Integral] Duvida sobre como começar
por effting » Ter Out 09, 2012 13:00
- 1 Respostas
- 1891 Exibições
- Última mensagem por effting

Ter Out 09, 2012 14:44
Cálculo: Limites, Derivadas e Integrais
-
- Integral - áreas
por Danilo » Sáb Nov 09, 2013 18:42
- 1 Respostas
- 2127 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Áreas
 por Danilo » Sex Nov 15, 2013 19:03
por Danilo » Sex Nov 15, 2013 19:03
- 2 Respostas
- 3519 Exibições
- Última mensagem por Man Utd

Qui Nov 21, 2013 17:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


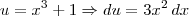 , e portanto a integral será
, e portanto a integral será  , basta colocar os limites de integração. Note que quando fazemos mudança de variável é necessário alterar os limites para que o valor final não se altere.
, basta colocar os limites de integração. Note que quando fazemos mudança de variável é necessário alterar os limites para que o valor final não se altere.
