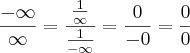por clarivando » Qua Dez 24, 2008 19:11
por clarivando » Qua Dez 24, 2008 19:11
Molina, para aplicar Hospital em
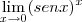
,

, fiz

= ln k e em seguida obtive ln k =
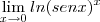
=

=

=

, ou seja, não consegui encontrar

e nem

, mas afinal, de alguma maneira, será que é possível aplicar D' Hospital nesse limite? Ah, e obrigado por me esclarecer que no limite ln0 tende a menos infinito!
-
clarivando
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Dez 21, 2008 20:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Molina » Qua Dez 24, 2008 21:12
por Molina » Qua Dez 24, 2008 21:12
Boa noite, Clarivando.
Primeiramente, de nada pela ajuda anterior. Sempre é bom analisar graficamente um limite.
Agora vamos a esta dúvida.
Antes de tudo, quando você D' Hospital nao queria dizer L'Hopital? O nome deve-se a esse matemático aqui:
http://pt.wikipedia.org/wiki/Guillaume_ ... C3%B4pital que publicou a regra que levou seu nome.
Neste caso acho que nao dá pra usar a regra, pelo menos nao entendi quando voce foi de \lim_{x\to0}\((senx)^x para ln\lim_{x\to0}\((senx)^x Se possível me explique melhor.
Já tentou usar a regra da cadeia?
Abraços e bom estudo!
Ah, e um feliz natal.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Guill » Dom Mai 27, 2012 16:47
por Guill » Dom Mai 27, 2012 16:47
Não é muito elegante aplicar o logaritmo neperiano no limite. Deve ser feito assim:
Seja y uma função tal que:

Podemos fazer:
![ln(y) = ln[(senx)^x] ln(y) = ln[(senx)^x]](/latexrender/pictures/51ea0dad84866b46c9745c7ce2a48e97.png)
Logo:
![\lim_{x\rightarrow 0} ln(y) = \lim_{x\rightarrow 0}ln[(senx)^x] \lim_{x\rightarrow 0} ln(y) = \lim_{x\rightarrow 0}ln[(senx)^x]](/latexrender/pictures/9a5709c033c0d3f6d7c76c220fc42a18.png)
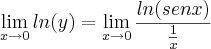
Esse é um caso onde se pode aplicar o Teorema de L'Hospital:
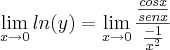

Podemos usar novamente o Teorema:

Uma vez que, quando

:

-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites, pode aplicar L'Hospital ?
por felipeemm » Sex Jul 31, 2015 00:13
- 1 Respostas
- 1462 Exibições
- Última mensagem por nakagumahissao

Sex Jul 31, 2015 11:45
Cálculo: Limites, Derivadas e Integrais
-
- Determinantes - cálculo matriz nxn (aplicar propriedades)
por emsbp » Qua Out 10, 2012 09:25
- 2 Respostas
- 3683 Exibições
- Última mensagem por emsbp

Qua Out 10, 2012 16:43
Matrizes e Determinantes
-
- Derivada- Como aplicar as formulas do quociente e do produto
por karinak » Sáb Jun 16, 2012 02:08
- 2 Respostas
- 1870 Exibições
- Última mensagem por karinak

Sáb Jun 16, 2012 12:43
Cálculo: Limites, Derivadas e Integrais
-
- Produtos Notáveis - como aplicar nesta equação
por fcomex » Ter Mai 20, 2014 00:15
- 1 Respostas
- 1305 Exibições
- Última mensagem por fcomex

Ter Mai 20, 2014 01:13
Álgebra Elementar
-
- Como aplicar o metodo de Gauss Jordan nesse sistema.
por 380625 » Sáb Ago 20, 2011 16:19
- 3 Respostas
- 6088 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 22:26
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
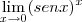 ,
,  , fiz
, fiz  = ln k e em seguida obtive ln k =
= ln k e em seguida obtive ln k = 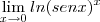 =
=  =
=  =
=  , ou seja, não consegui encontrar
, ou seja, não consegui encontrar  e nem
e nem  , mas afinal, de alguma maneira, será que é possível aplicar D' Hospital nesse limite? Ah, e obrigado por me esclarecer que no limite ln0 tende a menos infinito!
, mas afinal, de alguma maneira, será que é possível aplicar D' Hospital nesse limite? Ah, e obrigado por me esclarecer que no limite ln0 tende a menos infinito!



![ln(y) = ln[(senx)^x] ln(y) = ln[(senx)^x]](/latexrender/pictures/51ea0dad84866b46c9745c7ce2a48e97.png)
![\lim_{x\rightarrow 0} ln(y) = \lim_{x\rightarrow 0}ln[(senx)^x] \lim_{x\rightarrow 0} ln(y) = \lim_{x\rightarrow 0}ln[(senx)^x]](/latexrender/pictures/9a5709c033c0d3f6d7c76c220fc42a18.png)
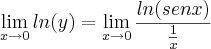
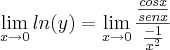


 :
: