 por paula luna » Ter Jun 28, 2011 19:21
por paula luna » Ter Jun 28, 2011 19:21
Oi, tava fazendo minha revisao pra prova e notei que esse exercicio ficou em branco, to quebrando a cabeça a quase 1hora e nao saio dele. Tentei ja aplicar a definiçao de modulo, tentei fazer regra da cadeia, mas nao saiu. Por favor se alguem puder RESOLVER este exercicio pra mim eu agradeço muito ou entao se me der uma dica realmente boa.
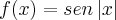
(seno do modulo de x)
f '(x) = ? (derivada da funçao f(x) - f linha de x -)
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Claudin » Ter Jun 28, 2011 19:51
por Claudin » Ter Jun 28, 2011 19:51
Estava errado meu raciocínio!
Analise a questão do módulo pela direita e pela esquerda.
sendo:
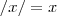
SE
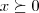

SE
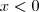
Editado pela última vez por
Claudin em Ter Jun 28, 2011 20:47, em um total de 3 vezes.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Ter Jun 28, 2011 20:06
por MarceloFantini » Ter Jun 28, 2011 20:06
Claudin, muito cuidado pois você escreveu uma tremenda besteira. O que ele quer é seno do módulo de x (ele inclusive deixou claro isso por extenso, não usando apenas a notação). Não existe função "sen".
A aplicação certa neste caso é a regra da cadeia:
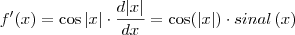
Onde
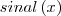
é a função sinal de x. Não tenho certeza nesta derivada, fiz uma pesquisa e não tive muita confiança nos resultados, mas espero que esteja certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por paula luna » Ter Jun 28, 2011 20:08
por paula luna » Ter Jun 28, 2011 20:08
Nao, calma acho que tu nao intendeu a funçao ou eu to pior do que pensava. A funçao é :
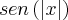
Ao menos é o que eu acho que é, pq na folha de atividades do meu professor ta
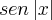
, mas ele normalmente so escreve no quadro sem o parenteses entao .... enfim eu tenho a resposta dessa atividade e talvez assim fique mais facil pra identificar qual é a funçao.
Resp:
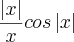
...
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Claudin » Ter Jun 28, 2011 20:30
por Claudin » Ter Jun 28, 2011 20:30
Irei ingressar na universidade agora em agosto e por isso não tenho toda certeza.
Mas o "futuro MATEMATICO" ja veio falando grosso, cantando de galo, espero que você esteja correto Marcelo.
Aqui no fórum somos amigos onde um ajuda o outro e não onde falamos que os outros fizeram "besteira", vai com calma!
abç
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Ter Jun 28, 2011 21:03
por Molina » Ter Jun 28, 2011 21:03
Boa noite.
Para resolver esta questão precisamos usar a regra da cadeia.
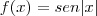
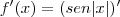
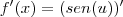
,onde
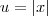
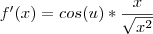 mas como u = |x| e raiz quadrada de x ao quadrado é igual a |x| tmabém...
mas como u = |x| e raiz quadrada de x ao quadrado é igual a |x| tmabém...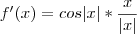
Paula, acho que você se confundiu na fração e trocou o numerador pelo denominador na sua resposta fornecida.
Caso sua dúvida seja na regra da cadeia, avise que o esclarecimento é rápido e fácil.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por paula luna » Ter Jun 28, 2011 21:35
por paula luna » Ter Jun 28, 2011 21:35
Nao nao, ta a resposta como eu falei mesmo. Mas eu tava pensando, |x| / x é , como disse o marcelo fantini la em cima, o sinal da derivada, entao tanto faz |x| / x ou x / |x|.
Ou seja, usando numeros como exemplo:
x = 2

=

= 1
x = -2
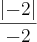
=
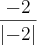
= -1
Nao sei mas acho que isso faz sentido ... e cheguei a conclusao que eu tinha conseguido fazer a questao sim, mas tava fazendo
![\sqrt[2]{{x}^{2}} \sqrt[2]{{x}^{2}}](/latexrender/pictures/8302b0b485da39090a74abac89c490c0.png)
= x ao inves de |x|.
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Jun 29, 2011 09:58
por LuizAquino » Qua Jun 29, 2011 09:58
Note que a função f(x) = |x| é equivalente a:
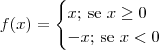
.
Se excluirmos o zero do domínio de f, criamos uma nova função g que é diferenciável em todos os pontos do seu domínio. Isto é, seja a função
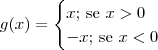
. A derivada de g é dada por:
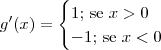
.
Note que a função g' pode ser reescrita como
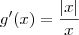
, ou ainda como
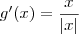
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12550 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10879 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13186 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14791 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5107 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
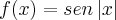 (seno do modulo de x)
(seno do modulo de x)
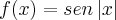 (seno do modulo de x)
(seno do modulo de x)
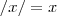 SE
SE 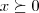
 SE
SE 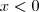

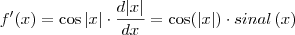
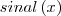 é a função sinal de x. Não tenho certeza nesta derivada, fiz uma pesquisa e não tive muita confiança nos resultados, mas espero que esteja certo.
é a função sinal de x. Não tenho certeza nesta derivada, fiz uma pesquisa e não tive muita confiança nos resultados, mas espero que esteja certo.

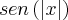
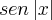 , mas ele normalmente so escreve no quadro sem o parenteses entao .... enfim eu tenho a resposta dessa atividade e talvez assim fique mais facil pra identificar qual é a funçao.
, mas ele normalmente so escreve no quadro sem o parenteses entao .... enfim eu tenho a resposta dessa atividade e talvez assim fique mais facil pra identificar qual é a funçao.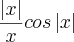


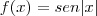
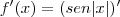
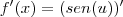 ,onde
,onde 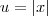
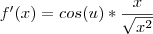
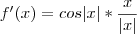


 =
=  = 1
= 1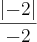 =
= 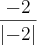 = -1
= -1![\sqrt[2]{{x}^{2}} \sqrt[2]{{x}^{2}}](/latexrender/pictures/8302b0b485da39090a74abac89c490c0.png) = x ao inves de |x|.
= x ao inves de |x|.
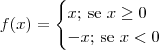 .
. . A derivada de g é dada por:
. A derivada de g é dada por: 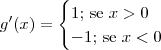 .
.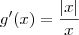 , ou ainda como
, ou ainda como 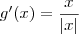 .
.