 por Deivid » Seg Jun 20, 2011 18:41
por Deivid » Seg Jun 20, 2011 18:41
Olá, eu estou com bastante dificuldades para resolver algumas questões de uma lista de exercícios que tenho aqui baseada no livro Cálculo B de Mirian Buss e Diva Flemming.
A questão é sobre máximos e mínimos e eu não sei nem como começar.
"Calcular as dimensões de uma caixa com base retangular, sem tampa, de volume máximo, com área lateral total igual a 5 cm²."
"Precisa-se construir um tanque com a forma de um paralelepípedo para estocar 270m³ de combustível, gastando a menor quantidade de material em sua construção. Supondo que todas as paredes são feitas do mesmo material e terão a mesma espessura, determinar as dimensões do tanque."
São as questões no estilo dessas duas que eu não consigo compreender. Alguém poderia dar uma luz?
Obrigado,
Deivid Steffens.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Seg Jun 20, 2011 19:54
por LuizAquino » Seg Jun 20, 2011 19:54
Para determinar o máximo ou o mínimo local de uma função de duas variáveis podemos usar o teste da segunda derivada.
Seja

. Suponha que
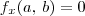
e

(com
f possuindo derivadas parciais contínuas até pelo menos a segunda ordem).
(i) Se
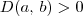
e

, então

é um mínimo local.
(ii) Se
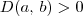
e

, então

é um máximo local.
(iii) Se
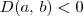
, então

não é nem mínimo e nem máximo local.
Desse modo, nesse tipo de exercício a primeira coisa que você precisa fazer é armar a função que deseja calcular o mínimo ou o máximo.
No caso particular dos exercícios que você enviou, note que essa parte de armar a função exige apenas os conhecimentos de Geometria Espacial. Portanto, é recomendável que você estude essa matéria caso não esteja sabendo.
SugestãoSe quiser revisar os conceitos de máximo ou mínimo de funções com uma variável, eu recomendo que assista as
vídeo-aulas:
- 19. Cálculo I - Máximo e Mínimo de Funções.
- 20. Cálculo I - Crescimento, Decrescimento e Concavidade do Gráfico de Funções.
- 21. Cálculo I - Teste da Primeira e da Segunda Derivada.
Editado pela última vez por
LuizAquino em Ter Jun 21, 2011 10:14, em um total de 4 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Deivid » Ter Jun 21, 2011 00:52
por Deivid » Ter Jun 21, 2011 00:52
Olá, obrigado pela resposta.
Seus vídeos me esclareceram algumas duvidas. Só para informar, eu tenho que resolver o exercício usando derivadas de mais variáveis, não uma.
Então analisando o primeiro problema eu tenho a informação que é uma caixa retangular, portanto volume é
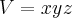
. E pela área informada eu obtenho
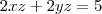
. A área total é

, portanto

.
Essas as informações que consegui coletar, estão corretas, como procedo agora?
Desculpe não conseguir avançar mais que isso, mas essa matéria realmente não entrou na minha cabeça.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Ter Jun 21, 2011 10:08
por LuizAquino » Ter Jun 21, 2011 10:08
Deivid escreveu:Então analisando o primeiro problema eu tenho a informação que é uma caixa retangular, portanto volume é V=xyz. E pela área informada eu obtenho 2xz + 2yz=5. A área total é At=Al + Ab, portanto At = 2xz + 2yz + xy.
O exercício informa que a
área lateral total é igual a 5 cm². Portanto, temos que 2xz + 2yz + xy = 5.
Queremos maximizar o volume, que é dado por V = xyz. Ora, essa é uma função de três variáveis, mas queremos utilizar os conhecimentos sobre o máximo de funções com duas variáveis.
Para reduzir o número de variáveis dessa função, basta perceber que da informação sobre a área lateral total temos que z = (5 - xy)/(2x + 2y). Portanto, V pode ser reescrito como uma função de duas variáveis:

.
Agora basta utilizar o teste da segunda derivada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Deivid » Qua Jun 22, 2011 17:06
por Deivid » Qua Jun 22, 2011 17:06
Infelizmente a primeira eu simplesmente não consegui fazer...
Mas a segunda eu consegui(tanque de 270m³), encontrei valores
![\left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right) \left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right)](/latexrender/pictures/f259531d86b480ab684525ac91dad146.png)
que coincidem com o da lista.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Jun 22, 2011 17:33
por LuizAquino » Qua Jun 22, 2011 17:33
Deivid escreveu:Infelizmente a primeira eu simplesmente não consegui fazer...
Que parte exatamente você não conseguiu fazer? Qual é exatamente a sua dúvida?
Você conseguiu calcular as derivadas parciais

e

?
Você conseguiu resolver o sistema abaixo?
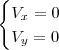
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por miguelfl » Qua Jun 22, 2011 21:21
por miguelfl » Qua Jun 22, 2011 21:21
é bom usar mutiplicadores de Lagrange, agora eu me confundi nessa parte das áreas laterias iguais a 5 porque aqui n dá quando eu coloco 2xy + 2 xz = 5
-
miguelfl
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 22, 2011 21:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por Deivid » Qua Jun 22, 2011 23:15
por Deivid » Qua Jun 22, 2011 23:15
Não sei o que são multiplicadores de lagrange, vou dar uma pesquisada. Na verdade a area das laterais é 2xz(a parte frontal e traseira) + 2 yz(as duas laterias) = 5.
Luiz Aquino, não havia percebido que você editou sua primeira mensagem, eu já conhecia esses conceitos do determinante e dos testes, não sabia apenas quando aplica-los.
Uma duvida, quando o determinante der maior que 0 e a derivada der = 0, existe essa possibilidade? (se não existe errei uma questão na prova hoje hehe)
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Qua Jun 22, 2011 23:44
por MarceloFantini » Qua Jun 22, 2011 23:44
Acredito que essa possibilidade não existe, pois segunda derivada igual a zero não se conclui nada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Jun 22, 2011 23:47
por LuizAquino » Qua Jun 22, 2011 23:47
miguelfl escreveu:(...) é bom usar mutiplicadores de Lagrange (...)
Acontece que os Multiplicadores de Lagrange tipicamente são abordados depois do conteúdo de máximo e mínimo de funções com várias variáveis. Por isso mesmo que eu não sugeri, pois pela primeira pergunta do Deivid percebe-se que ele ainda não estudou esse conteúdo, como de fato ele acabou confirmando.
miguelfl escreveu:agora eu me confundi nessa parte das áreas laterias iguais a 5 porque aqui n dá quando eu coloco 2xy + 2 xz = 5
Deivid escreveu:Na verdade a area das laterais é 2xz(a parte frontal e traseira) + 2 yz(as duas laterias) = 5.
O exercício diz que a área lateral
total é 5 cm². É para contabilizar a parte frontal, traseira, laterais e o fundo. Só não é para contabilizar a tampa, como sugere o texto do exercício. Por isso que ficamos com 2xz + 2yz + xy = 5.
Em verdade, o texto do exercício deveria estar mais claro. Por exemplo, poderia estar escrito que a superfície (ou a área) total da caixa é 5 cm².
ObservaçãoNa minha primeira mensagem, onde há escrito
Seja

.
leia-se
Seja

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [maximos e minimos] Problemas de minimos e maximos
por amigao » Seg Jun 24, 2013 22:28
- 1 Respostas
- 3809 Exibições
- Última mensagem por young_jedi

Ter Jun 25, 2013 17:49
Cálculo: Limites, Derivadas e Integrais
-
- Maximos e minimos
por Maykids » Qui Jun 02, 2011 01:30
- 1 Respostas
- 1501 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 15:17
Cálculo: Limites, Derivadas e Integrais
-
- Problema, mínimos e máximos
por Bruhh » Sex Jun 11, 2010 16:45
- 3 Respostas
- 2692 Exibições
- Última mensagem por Bruhh

Sex Jun 11, 2010 16:53
Cálculo: Limites, Derivadas e Integrais
-
- Minimos e Maximos locais
por aline_n » Seg Jun 06, 2011 22:36
- 1 Respostas
- 1345 Exibições
- Última mensagem por LuizAquino

Ter Jun 07, 2011 11:32
Cálculo: Limites, Derivadas e Integrais
-
- Otimização (Maximos e Minimos)
por Maykids » Sex Jun 24, 2011 03:49
- 4 Respostas
- 3996 Exibições
- Última mensagem por LuizAquino

Sáb Jun 25, 2011 16:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Suponha que
. Suponha que 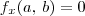 e
e  (com
(com 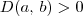 e
e  , então
, então  é um mínimo local.
é um mínimo local. , então
, então 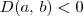 , então
, então 
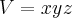 . E pela área informada eu obtenho
. E pela área informada eu obtenho 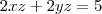 . A área total é
. A área total é  , portanto
, portanto  .
. .
.![\left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right) \left(3\sqrt[3]{10}, 3\sqrt[3]{10}, 3\sqrt[3]{10} \right)](/latexrender/pictures/f259531d86b480ab684525ac91dad146.png) que coincidem com o da lista.
que coincidem com o da lista. e
e  ?
?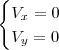


 .
.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
