Primeiro, note que o volume irá depender de duas variáveis:
- b -- medida dos lados do quadrado da base;
- h -- medida da altura.
A área também irá depender dessas duas variáveis.
Considere que E é o custo na construção da tampa e do fundo do reservatório. Considere também que L é o custo na construção da lateral. Desse modo, o custo C será dado por C = 2E + L.
Mas, como você tem a informação de quanto é o volume, você pode colocar h em função de b (ou o contrário se desejar).
Se você decidir colocar h em função de b, então a sua função custo será algo do tipo C(b).
Desse modo, primeiro você precisará calcular C'(b) = 0 para determinar os pontos críticos de C. Em seguida, você deverá analisar o sinal de C''(b) avaliada nos pontos críticos.
ObservaçãoVocê escreveu:
(...) construção da tampa da laje de fundo (...)
Mas, não seria "
construção da tampa e da laje de fundo"?







 ;
; ;
;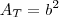 ;
; .
. (nesse contexto,
(nesse contexto,  custa 1 unidade monetária por m² e
custa 1 unidade monetária por m² e  custa 2 unidades).
custa 2 unidades).




 .
.
 :
: