 por Claudin » Sáb Mai 14, 2011 17:01
por Claudin » Sáb Mai 14, 2011 17:01
Gostaria de saber como resolver esse limite!
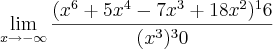
obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Sáb Mai 14, 2011 18:20
por Molina » Sáb Mai 14, 2011 18:20
Boa tarde.
Quando você escrever potência no LaTeX e o expoente tiver dois ou mais algarismos há a necessidade de coloca-lo entre { }. Senão fica apenas o primeiro algarismo considerado um expoente.
Claudin escreveu:Gostaria de saber como resolver esse limite!
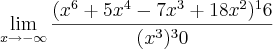
obrigado
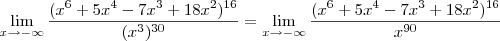
Perceba que elevando o numerador terá uma estrutura assim:
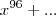
onde as outras partes literais são menores do que
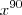
.
Ou seja, dividindo o numerador e o denominador por
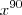
temos uma estrutura assim:


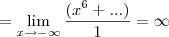
Perceba que a parte dos
três pontos (...) ficará do tipo
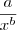
, onde a é um número real e b um valor positivo. Quando

este valor tende a 0, por isso chegamos no
limite igual a infinito.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Dom Mai 15, 2011 11:57
por Claudin » Dom Mai 15, 2011 11:57
Obrigado pela ajuda!
Deu pra compreender agora.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE] Exercício em que o limite não existe!
por mih123 » Qua Ago 29, 2012 17:14
- 3 Respostas
- 2422 Exibições
- Última mensagem por e8group

Sex Ago 31, 2012 12:21
Cálculo: Limites, Derivadas e Integrais
-
- Exercício Limite
por Claudin » Sáb Mai 21, 2011 16:34
- 3 Respostas
- 1841 Exibições
- Última mensagem por Claudin

Ter Mai 24, 2011 11:52
Cálculo: Limites, Derivadas e Integrais
-
- exercício de Limite
por jr_freitas » Qui Out 06, 2011 11:56
- 7 Respostas
- 3463 Exibições
- Última mensagem por moyses

Sex Out 07, 2011 11:33
Cálculo: Limites, Derivadas e Integrais
-
- Exercício {limite}
por Danilo » Qua Abr 10, 2013 23:16
- 2 Respostas
- 1409 Exibições
- Última mensagem por Danilo

Ter Abr 23, 2013 11:44
Cálculo: Limites, Derivadas e Integrais
-
- {limite} Exercicio
por dehcalegari » Seg Abr 15, 2013 12:59
- 2 Respostas
- 1174 Exibições
- Última mensagem por dehcalegari

Seg Abr 15, 2013 13:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
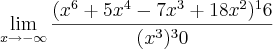

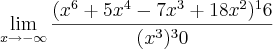

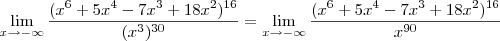
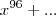 onde as outras partes literais são menores do que
onde as outras partes literais são menores do que 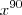 .
.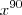 temos uma estrutura assim:
temos uma estrutura assim:

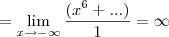
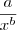 , onde a é um número real e b um valor positivo. Quando
, onde a é um número real e b um valor positivo. Quando  este valor tende a 0, por isso chegamos no limite igual a infinito.
este valor tende a 0, por isso chegamos no limite igual a infinito.

