Já tentei exaustivamente mas não consegui resolver a questão que segue abaixo:
f: R em R é a função dada por
, nessa função o (cost) está elevado à sexta potência, e não apenas a variável "t".Nesse caso f ' (0) = 4 . Verdadeiro ou falso?
A minha dificuldade está no fato de que dentro da integral a variável é "t", enquanto que o "x" aparece em um dos limites de integração.
Gostaria de entender como essa questão pode ser resolvida.
Agradeço desde já a atenção dispensada.
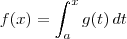, com 
constante, então 
. Então, derivando 
você terá a função da integral como uma função de x, logo basta substituir por zero e ver se é verdadeiro.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)