 por Cristiano Tavares » Qua Mai 11, 2011 22:16
por Cristiano Tavares » Qua Mai 11, 2011 22:16
Olá a todos,
Já tentei exaustivamente mas não consegui resolver a questão que segue abaixo:
f: R em R é a função dada por

, nessa função o (cost) está elevado à sexta potência, e não apenas a variável "t".
Nesse caso f ' (0) = 4 . Verdadeiro ou falso?
A minha dificuldade está no fato de que dentro da integral a variável é "t", enquanto que o "x" aparece em um dos limites de integração.
Gostaria de entender como essa questão pode ser resolvida.
Agradeço desde já a atenção dispensada.
-
Cristiano Tavares
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 11, 2011 21:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
 por MarceloFantini » Qua Mai 11, 2011 23:35
por MarceloFantini » Qua Mai 11, 2011 23:35
Não é para resolver a integral. Pelo teorema fundamental do cálculo, quando
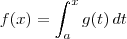
, com

constante, então

. Então, derivando

você terá a função da integral como uma função de x, logo basta substituir por zero e ver se é verdadeiro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cristiano Tavares » Qua Mai 11, 2011 23:59
por Cristiano Tavares » Qua Mai 11, 2011 23:59
Marcelo,
Muito obrigado pela ajuda, sua resposta foi rápida, clara e objetiva. Um abraço!
-
Cristiano Tavares
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 11, 2011 21:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 3133 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
-
- Não consigo resolver essa questão com derivada
por Cristiano Tavares » Sáb Jun 18, 2011 12:18
- 2 Respostas
- 1833 Exibições
- Última mensagem por Cristiano Tavares

Sáb Jun 18, 2011 15:07
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa integral.
por 380625 » Qua Set 07, 2011 14:02
- 3 Respostas
- 3110 Exibições
- Última mensagem por Neperiano

Qua Set 07, 2011 15:37
Cálculo: Limites, Derivadas e Integrais
-
- Alguém pode me ajudar a resolver essa integral?
por V_Netto » Seg Jul 30, 2012 12:05
- 1 Respostas
- 1886 Exibições
- Última mensagem por Russman

Seg Jul 30, 2012 12:54
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo calcular essa derivada!!!
por Catalao » Qua Mai 09, 2012 19:51
- 3 Respostas
- 2366 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , nessa função o (cost) está elevado à sexta potência, e não apenas a variável "t".
, nessa função o (cost) está elevado à sexta potência, e não apenas a variável "t".

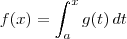 , com
, com  constante, então
constante, então  . Então, derivando
. Então, derivando  você terá a função da integral como uma função de x, logo basta substituir por zero e ver se é verdadeiro.
você terá a função da integral como uma função de x, logo basta substituir por zero e ver se é verdadeiro.



 , avisa que eu resolvo.
, avisa que eu resolvo.

