Bom, estou fazendo um trabalho no qual eu tenho que calcular o volume de um sólido de forma aproximada
(soma de Riemann) e de forma exata (integral).
Já fiz um trabalho muito semelhante a este algum tempo atrás e por este motivo acho que estou resolvendo de forma errada
já que os valores estão muito diferentes. Vamos ao meu dilema:
A função é:

Sendo que:
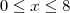
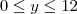

Utilizando o ponto médio.
Então para a soma de Riemann fiz: f(0,5 ; 0,5) + f(0,5 ; 1,5) + f(0,5 ; 2,5) ... + f(7,5 ; 11,5).
Somando todas essas funções obtive V=582,830221 cm³
Então resolvi a integral:

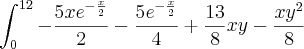

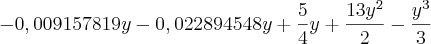
=374,6153716 cm³
O outro trabalho que eu resolvi, também pelo ponto médio, deu uma diferença menor que 1.
Como os valore são quase o dobro um do outro creio que algo está errado mas não sei o que.
Por favor alguém me ajuda, é muito importante!!
Muito Obrigada


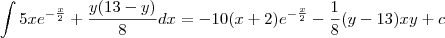 , com
, com 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
